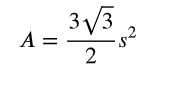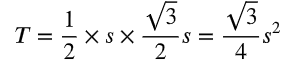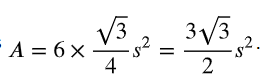Actualizado 4 diciembre, 2020
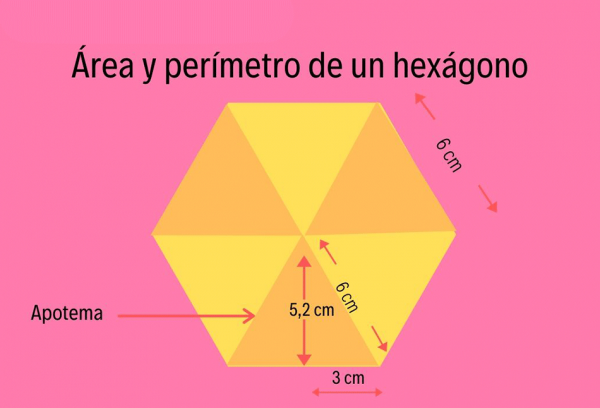
Un hexágono es una figura geométrica que se encuentra comúnmente en la vida cotidiana, lo podemos encontrar por ejemplo en un panal, en una tela de araña, en una tuerca y tornillo, entre otros. A continuación les explicaremos qué es un hexágonos, qué tipos existen y cómo se calcula el perímetro y el área del mismo.
¿Qué es un hexágono?
Algunas formas se encuentran en toda la naturaleza, y el hexágono es una de ellas. Este es una figura geométrica bidimensional de 6 lados (todos ellos son rectos, no curvos). Los hexágonos se encuentran en panales creados por las abejas para almacenar miel, polen y larvas. Incluso se encuentran en las famosas columnas entrelazadas de roca volcánica que forman la Calzada del Gigante en Irlanda. Si bien estos ejemplos pueden ser los más conocidos, los hexágonos se encuentran en muchas otras partes de la naturaleza: las formas de enlace de ciertas moléculas, en las estructuras cristalinas, en los patrones de los caparazones de las tortugas y más.
Pero, ¿por qué hexágonos? ¿Qué tienen de especial? Bueno, todo es cuestión de eficiencia. Si crea una cuadrícula de hexágonos, las formas se entrelazan perfectamente, sin absolutamente ningún espacio. Pero en comparación con otras formas que se entrelazan así, las líneas de cada hexágono son tan cortas como pueden ser. Cualquier otra forma entrelazada tendrá líneas más largas. El resultado de esto es que requieren menos materiales para construir y tienen mucha resistencia a la compresión.
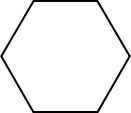
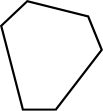
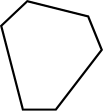
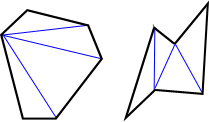
Un hexágono es un polígono con 6 lados y 6 ángulos (hexa- significa seis). En la siguiente figura hay 3 tipos diferentes de hexágonos.
Tipos de exágonos
Como otros polígonos, un hexágono puede clasificarse como regular o irregular. Si todos los lados y ángulos interiores de un hexágono son iguales, es un hexágono regular. De lo contrario, es un hexágono irregular.
Hexágono regular
Todos los lados y ángulos interiores son iguales
Hexágono irregular
No todos los lados y ángulos son iguales
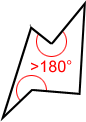
Los hexágonos u otros polígonos también se pueden clasificar como convexos o cóncavos. Si todos los ángulos interiores de un hexágono o polígono son menores de 180°, es convexo. Si uno o más ángulos interiores son mayores de 180°, es cóncavo. Un hexágono regular es siempre un hexágono convexo.
Hexágono convexo
Todos los ángulos interiores <180 °
Hexágono cóncavo
Uno o más ángulos interiores> 180 °
Diagonales de un hexágono
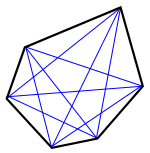
Una diagonal es un segmento de línea que une dos vértices no consecutivos. Se pueden dibujar tres diagonales de cada vértice, formando un total de nueve diagonales para un hexágono. La siguiente figura no lo ejemplificará:
Ángulos internos de un hexágono
La suma de los ángulos interiores de un hexágono es igual a 720°.
Como se muestra en la figura anterior, se pueden dibujar tres diagonales para dividir el hexágono en cuatro triángulos. Las líneas azules de arriba muestran solo una forma de dividir el hexágono en triángulos; pero hay otras. La suma de los ángulos interiores de los cuatro triángulos es igual a la suma de los ángulos interiores del hexágono. Dado que la suma de los ángulos interiores de un triángulo es 180°, la suma de los ángulos interiores del hexágono es 4 × 180° = 720°.
Hexágono regular
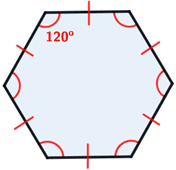
Un hexágono regular es un hexágono en el que todos los lados tienen la misma longitud y todos los ángulos interiores tienen la misma medida.
Ángulos y lados de un hexágono regular
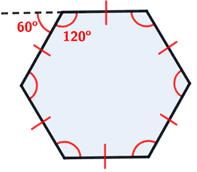
Dado que cada uno de los seis ángulos interiores de un hexágono regular tiene la misma medida, cada ángulo interior mide 720 ° / 6 = 120 °, como se muestra a continuación.
Cada ángulo exterior de un hexágono regular tiene una medida igual de 60 °.
Los lados de un hexágono regular tienen la misma longitud y los lados opuestos son paralelos.
AB = BC = CD = DE = EF = FA y AB // DE, BC // EF, CD // FA
Simetría en un hexágono regular
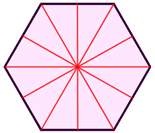
Un hexágono regular tiene 6 líneas de simetría y una simetría rotacional de orden 6, lo que significa que se puede rotar de tal manera que se verá igual que la forma original 6 veces en 360°.
Lineas de simetría
Simetría rotacional
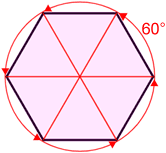
Seis ángulos de rotación de 60 °
Área de un hexágono regular
El área de un hexágono regular con longitud de lado s es:
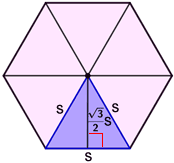
Desde el centro, un hexágono regular se puede dividir en seis triángulos equiláteros, cada uno con una longitud de lado, s, como se muestra a continuación.
El área, T, de uno de los triángulos equiláteros, dibujados en azul, se puede encontrar usando:
Donde la apotema es la altura del triángulo. Como hay seis triángulos equiláteros, el área de un hexágono regular es
Perímetro de un hexágono
El hexágono se puede cortar en seis triángulos equiláteros, todos del mismo tamaño. Debido a que estos son triángulos equiláteros, sus lados tienen todos la misma longitud. Entonces, los lados de un hexágono también tienen la misma longitud.
El perímetro de un hexágono es la suma de las longitudes de todos los lados. Todos los lados tienen la misma longitud, por lo que es lo mismo que la longitud de un lado multiplicada por seis.
Propiedades de un hexágono regular
- Tiene seis lados y seis ángulos.
- Las longitudes de todos los lados y la medida de todos los ángulos son iguales.
- El número total de diagonales en un hexágono regular es 9.
- La suma de todos los ángulos interiores es igual a 720 grados, donde cada ángulo interior mide 120 grados.
- La suma de todos los ángulos exteriores es igual a 360 grados, donde cada ángulo exterior mide 60 grados.
Ejercicios de hexágonos
Pregunta 1: Calcula el área y el perímetro de un hexágono regular cuyo lado mide 4.1 cm.
Solución:
Dado, lado del hexágono = 4,1 cm
Área de un hexágono = {(3x√3)/2}/ × a^2
Área de un hexágono = {(3x√3)/2}/ × 4.1^2 = 43.67 cm
Perímetro del hexágono = 6a = 6 × 4.1 = 24.6 cm
Pregunta 2: El perímetro de una tabla hexagonal mide 24 cm. Encuentra el área del tablero.
Solución:
Dado, perímetro del tablero = 24 cm
Perímetro de un hexágono = 6a
24 cm = 6a
a = 24/6 = 4 cm
Área de un hexágono = {(3x√3)/2}/ × 4^2 = 41.57 cm²
Hemos llegado al final de nuestro artículo sobre los hexágonos. Esperamos que haya comprendido el tema en su totalidad y no tenga ninguna duda. Caso contrario, déjenos un comentario debajo, estaremos contentos de ayudarlo.
Hasta pronto!!!