Actualizado 26 septiembre, 2020
De todas las formas y figuras geométricas existentes, el círculo es una de las más fascinantes presentes a nuestro alrededor. Ya sea el sol, la luna e incluso la tapa de una botella, los objetos circulares son bastante comunes. Intentemos comprender su definición, seguido de las fórmulas necesarias para calcular el diámetro, el área, entre otros diversos aspectos asociados con la geometría.
Definición de círculo
Un círculo es una forma en la que todos los puntos tienen la misma distancia del centro. Algunos ejemplos del mundo real incluyen a una rueda, un plato, una moneda, etc. Dibujarlo correctamente no es fácil a mano alzada, por lo que la mayoría de la gente prefiere la utilización de un compás (una herramienta geométrica), ya sea en la escuela o en el lugar de trabajo.
Términos importantes relacionados con el círculo
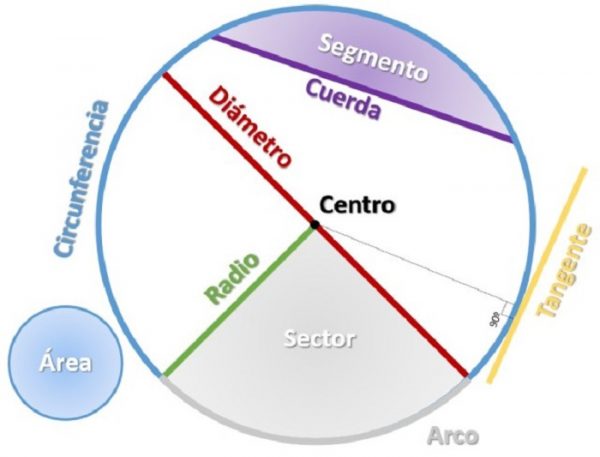
Diámetro
El diámetro se puede denominar como una línea que se traza a través de un círculo y que pasa por el centro.
Radio
Es la distancia desde el medio o el centro de un círculo hacia cualquier punto. Curiosamente, cuando colocas dos radios uno al lado del otro, la resultante tendría la misma longitud que el diámetro. Por lo tanto, podemos llamar a un diámetro el doble de largo que el radio en cuestión.
Área del círculo
En un círculo, el área se puede expresar como π por el cuadrado del radio. Está escrito como: A = π x r^2. Teniendo en cuenta el diámetro: A = (π / 4) × D2
Cuerda
Un segmento de línea que une dos puntos presentes en una curva se denomina cuerda. En geometría, la utilidad de una cuerda se centra en describir un segmento que conecta dos extremos sobre un círculo.
Tangente y arco
Una línea que toca ligeramente el círculo en su viaje en una dirección diferente es Tangente. Por otro lado, una parte de la circunferencia es un Arco.
Sector y segmento
Un sector es una parte de un círculo rodeado por dos radios junto con su arco interceptado. El segmento es la región que está encerrada por una cuerda junto con el arco subtendido por la cuerda.
Sectores comunes
En geometría, el cuadrante y el semicírculo son dos versiones especiales de un sector.
- El cuarto de un círculo se denomina Cuadrante.
- La mitad de un círculo se conoce como semicírculo.
Cómo dibujar un círculo
- Tome una hoja de papel y marque un solo punto en la hoja, en algún lugar en el medio de la misma, y asígnele el nombre al punto O.
- Seleccione una longitud aleatoria para el radio, por ejemplo, 3 cm.
- Con una regla, mantenga la marca cero de referencia en el punto O y marque al azar a 3 cm del punto O en una la dirección.
- Marque tantos puntos como desee alejados del punto O, pero todos ellos deben estar exactamente a 3 cm del mismo.
- Si ha seleccionado suficientes puntos, puede notar que la forma comienza a parecerse a un círculo y esta es exactamente la definición de un círculo.
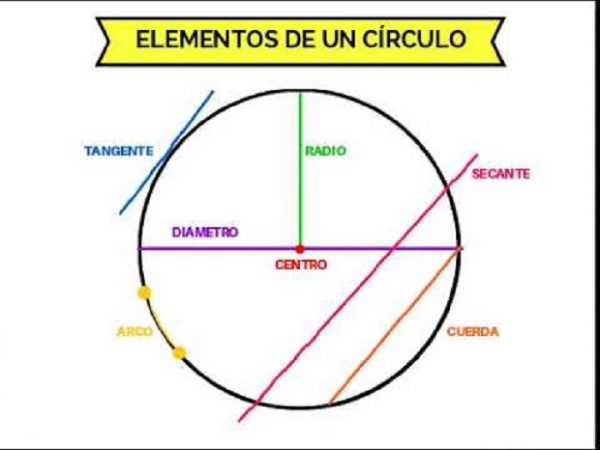
Terminologías de círculos
- Anillo: la región delimitada por dos círculos concéntricos. Básicamente es un objeto con forma de anillo.
- Arco: es básicamente la curva conectada de un círculo.
- Sector: una región delimitada por dos radios y un arco.
- Segmento: una región delimitada por una cuerda y un arco que se encuentra entre los extremos de la cuerda. Cabe señalar que los segmentos no contienen el centro.
- Centro: es el punto medio de un círculo.
- Cuerda: un segmento cuyos extremos se encuentran en el círculo.
- Diámetro: un segmento que tiene ambos puntos extremos en el círculo y es la cuerda más grande del mismo.
- Radio: un segmento que conecta el centro de un círculo con cualquier punto del mismo.
- Secante: una línea recta que corta el círculo en dos puntos. También se llama cuerda extendida.
- Tangente: una línea recta coplanar que toca el círculo en un solo punto.
Propiedades y aspectos clave
Centrándonos en la geometría, existen numerosos hechos asociados con los círculos. Además, también se puede probar su relación con líneas rectas, polígonos y ángulos. Todos estos hechos juntos son propiedades del círculo. Intentemos aprender las principales para mejorar nuestro conocimiento.
1. Se sabe que los círculos que tienen radios iguales son congruentes.
2. Para su sorpresa, los círculos con diferentes radios se consideran similares.
3. En un círculo, se sabe que el ángulo central que intercepta un arco es el doble de cualquier ángulo inscrito que intercepte el mismo arco.
4. Se sabe que las cuerdas que son equidistantes del centro tienen la misma longitud.
5. Un radio perpendicular a una cuerda en particular la divide.
6. La tangente siempre forma un ángulo recto con el radio considerando el punto de contacto.
7. Dos tangentes que se dibujan en un círculo desde un punto exterior tienen la misma longitud.
8. La circunferencia de dos círculos diversos es proporcional a los radios correspondientes.
9. Se sabe que el ángulo subtendido en el centro del círculo por su circunferencia es equivalente a cuatro ángulos rectos.
10. Los arcos asociados al mismo círculo se denominan proporcionales a sus ángulos correspondientes.
11. Las cuerdas iguales tienen circunferencias iguales.
12. Los círculos iguales tienen circunferencias iguales.
13. Se sabe que los radios vinculados a círculos iguales son iguales.
14. La cuerda más larga es el diámetro.
Ejercicios para practicar
Pregunta 1. Calcule el área de un círculo que tiene un radio de 1.2 m.
Respuesta:
El área aquí se puede calcular usando la fórmula, Área = π x r^2
Por lo tanto, A = π × 1.2^2
= 3,14159… × (1,2 × 1,2)
= 4.52 (a 2 decimales).
Pregunta 2: ¿Cómo encuentras el área del círculo?
Respuesta: La fórmula para encontrar el área del círculo es π x r^2. Además, puedes encontrar el área de un círculo multiplicando el valor de pi que es 3.14 o 22/7 por el cuadrado del radio. Sin embargo, en lugar del radio, el diámetro de un círculo se menciona en la pregunta y luego la mitad, ya que el radio es la mitad del diámetro.
Pregunta 3: ¿La circunferencia de un círculo es cuadrada?
Respuesta: Por lo general, podemos definir pi como la relación entre la circunferencia de un círculo y su diámetro, por lo tanto, la circunferencia de un círculo es pi por el diámetro o 2 pi por el radio. Entonces, esto proporciona una prueba geométrica de que el área del círculo realmente es π x r^2.
Pregunta 4: ¿Puedes dar una definición simple de un círculo?
Respuesta: Se refiere a una forma 2D redonda en la que todos los puntos del borde del círculo están a la misma distancia del centro. Además, el diámetro de un círculo es igual al doble de su radio. A su vez, la circunferencia de un círculo es la línea que rodea el centro del círculo.
Pregunta 5: Defina el radio de un círculo
Respuesta: Se refiere a la distancia entre los centros a cualquier punto de su circunferencia. La forma más sencilla de encontrar el radio es la mitad del diámetro.