Actualizado 24 noviembre, 2020
El rombo es una figura geométrica plana donde sus cuatro lados son de misma longitud y los ángulos interiores opuestos son iguales.
A continuación conoceremos acerca de esta popular figura geométrica.

¿Qué es un Rombo?
El rombo es una figura que consta de dos ángulos que son mayores que el otro par y donde sus lados son iguales. Esta figura geométrica plana es un cuadrilátero, es decir que tiene cuadro lados y a su vez es un paralelogramo, concepto que implica que todos sus lados poseen la misma longitud.
El rombo a diferencia del cuadrado y del rectángulo, no tiene ángulos rectos, sus ángulos son oblicuos y esto se debe a que sus rectas están ligeramente inclinadas y no son perpendiculares entre ellas.
Se incluye a los rombos en la categoría de los polígonos. Estas son figuras planas que se forman por una cantidad infinita de segmentos rectos dispuestos de manera consecutiva en el plano. Estos segmentos se denominan lados, y como el rombo tiene cuatro lados es que se lo califica como un cuadrilátero.
Dentro de esta clasificación de cuadrilátero, el rombo es un paralelogramo, es decir que tiene lados paralelos y lados opuestos que son iguales.
Resumiendo podemos decir que el rombo es un polígono, cuadrilátero y paralelogramo, en donde todos sus lados son iguales y dos de sus ángulos son mayores que los otros dos.
Características del rombo
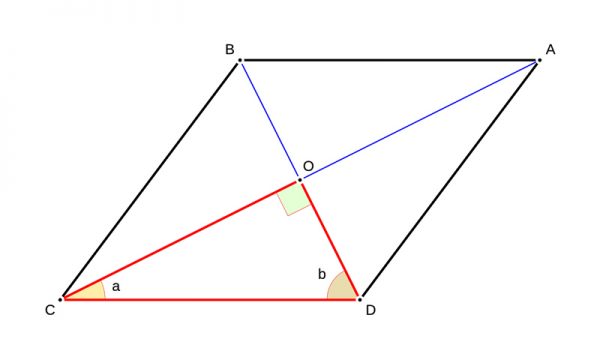
El rombo consiste en la unión de sus lados por cuatro puntos llamados vértices. Los ángulos internos de esta figura geométrica son diferentes a 90° y los ángulos opuestos son iguales a 90°, esto implica que posee 2 ángulos agudos y 2 ángulos obtusos.
Otra de sus características es que sus diagonales son perpendiculares entre si y se intersecan en el incentro. Sus dos alturas poseen la misma longitud que el diámetro de la circunferencia. El incentro es el punto en el cual las tres bisectrices de sus ángulos internos se cortan, y además es el punto central de la circunferencia del rombo.
La bisectriz es la recta que toca el vértice de un ángulo y lo corta en parte iguales. La circunferencia inscrita es la que se puede dibujar dentro de un polígono de maneta tal que toque todos sus lados.
Entre las principales características o propiedades que tiene un rombo podemos encontrar:
-Tiene cuatro lados de igual longitud.
-Los cuatro ángulos que son iguales dos a dos, esto quiere decir que sus ángulos opuestos tienen la misma medida.
-La suma de sus ángulos, como en cualquier cuadrilátero es de 360°.
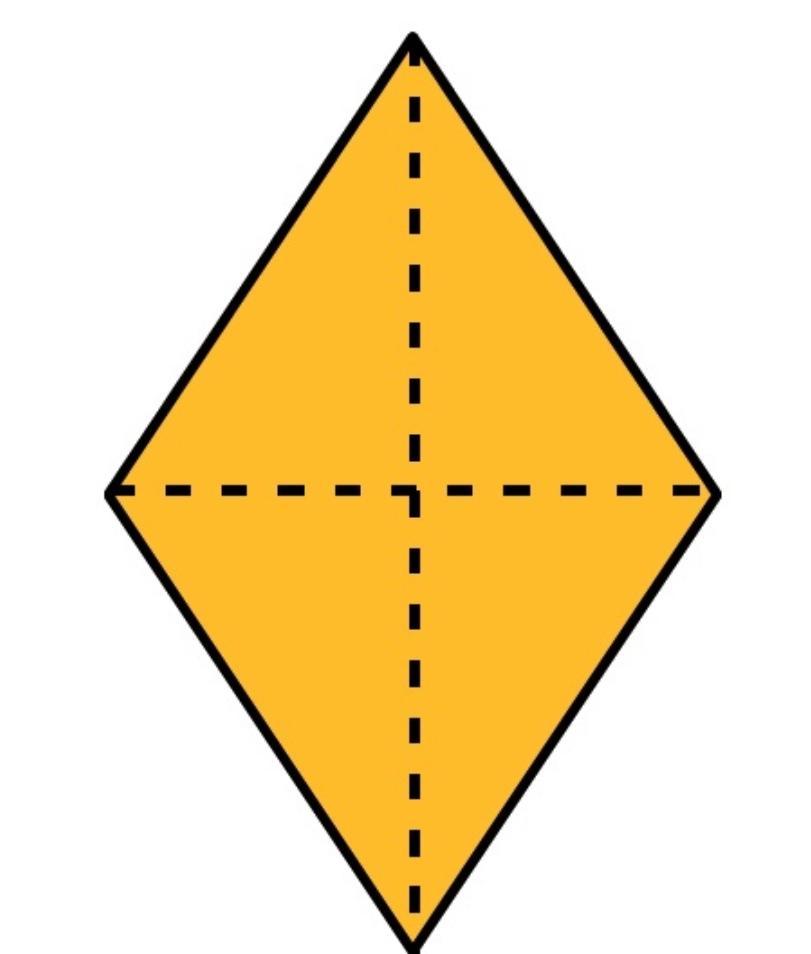
-Tiene dos ejes de simetría.
-Las diagonales se bisecan en el ángulo recto y son bisectrices de sus ángulos.
-El incentro de la figura es el punto en donde cortan las diagonales y la división del mismo permite obtener partes iguales.
-Si sumamos los lados adyacentes de la figura, obtendremos el resultado es 180°. Esto implica que sus ángulos adyacentes son complementarios.
-No existen diferentes tipos de rombo.
-El diámetro y la alturas son la medida de la separación entre lados paralelos opuestos.
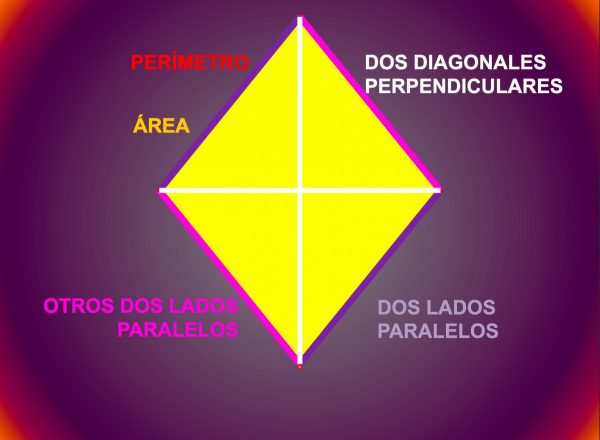
Diagonal de un rombo
Tal como detallábamos el rombo posee dos diagonales que se cortan en el centro formando un ángulo recto, esto implica que las diagonales del rombo son perpendiculares.
¿Cómo calcular el número de diagonales de un rombo?
La fórmula para saber el número de diagonales del rombo es:
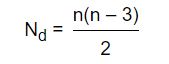
Donde: Nd es el número de diagonales y n es el número de lados.
Como el rombo tiene 4 lados, sabremos que n = 4 y sustituyendo en nuestra fórmula obtendremos como resultado que el número de diagonales del rombo será igual a 2:
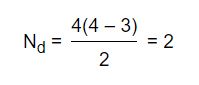
¿Cómo calcular la diagonal de un rombo?
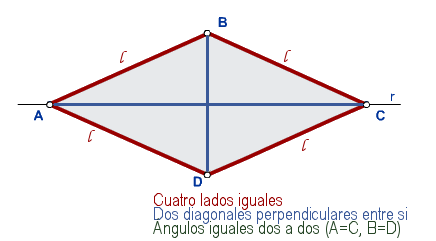
Al mirar la perpendicular de las diagonales se puede observar que se forma un triángulo rectángulo, por lo que un lado (a) sería la hipotenusa y las diagonales D1 y D2 son los catetos. De este modo aplicando el Teorema de Pitágoras podremos encontrar las diagonales de un rombo.
Perímetro de un rombo
Dependiendo de las variables conocidas es posible calcular el perímetro del rombo.
-Calcular el perímetro del rombo conociendo un lado: El perímetro de un rombo es igual a la suma de sus lados:
Perímetro = a + a + a + a
Como sus cuatro lados poseen la misma longitud, el perímetro es cuatro veces uno de sus lados: Perímetro = 4a
-Calcular el perímetro del rombo conociendo sus diagonales: despejando la fórmula para encontrar la diagonal del rombo en relación a la variable a. En este caso “a” corresponde a la hipotenusa del triángulo rectángulo, por lo tanto la fórmula será:
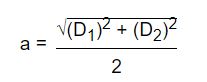
Sustituyendo la anterior ecuación en la fórmula del perímetro = 4a, obtendremos:
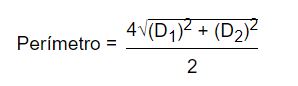
Área de un rombo
Se puede calcular el área de un rombo, dependiendo de las variables conocidas.
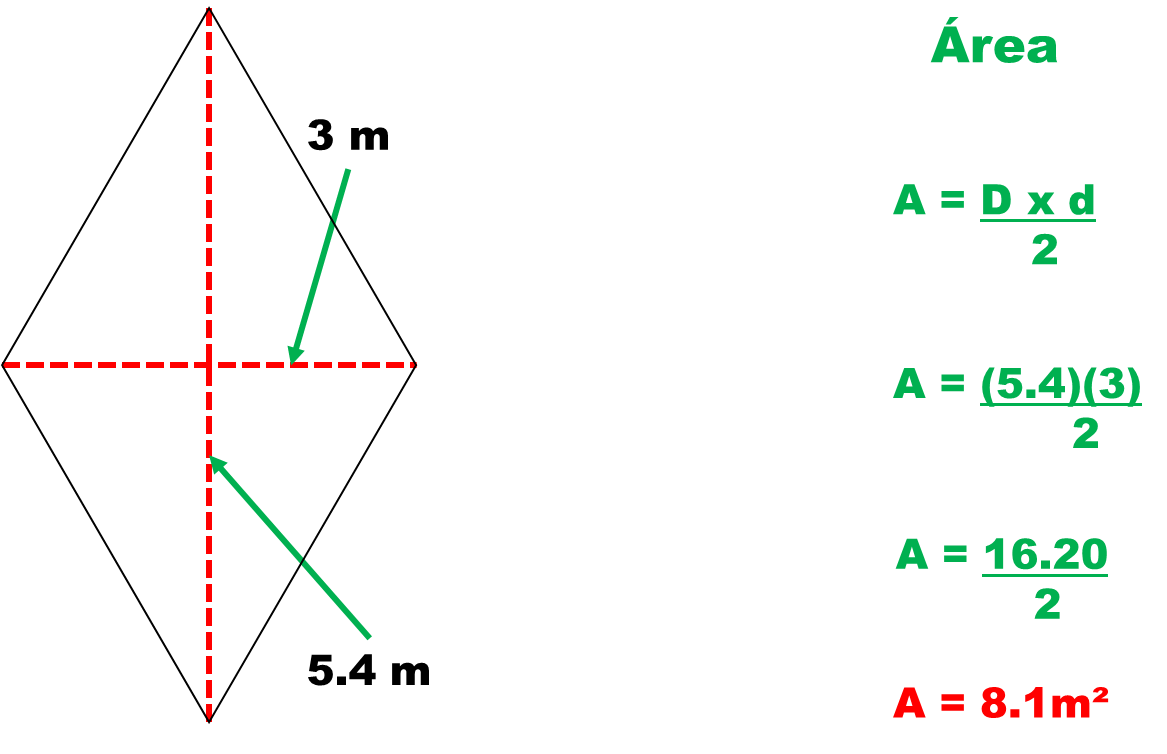
-Para calcular el área del rombo conociendo sus diagonales: lo haremos por medio del producto de las diagonales D1 y D2 y dividiendo entre 2.
– Para calcular el área del rombo conociendo un lado y la altura: consideramos a un lado (a) como la base del rombo y la altura se considera desde la línea paralela a la base. De esta forma la fórmula es el producto de base por la altura: Área = (a)(h)
Diferencia entre Rombo y Romboide
Más allá de que sus nombres suenen similares y ambos pertenezcan al grupo de los paralelogramos, debemos saber que ambas figuras geométricas no son iguales. Dentro de su principal diferencia podemos decir que:
El rombo posee cuatro lados iguales y sus diagonales se cortan perpendicularmente. En cambio el romboide solo tiene sus lados opuestos iguales (como el rectángulo) y sus diagonales no son perpendiculares entre si.
Presencia del rombo en otros ámbitos
Tal como detallábamos uno de los aspectos importantes que caracterizan al rombo es la existencia de paralelismo entre sus lados. Los lados que se oponen son paralelos entre si, a pesar de que la distancia entre ellos puede ir variando según el tipo de rombo que sea.
Junto con los cuadrados y los triángulos, se considera al rombo como una de las figuras geométricas más comunes y simples de analizar, ya que todos sus lados son equivalentes entre si y por ende la suma de sus ángulos y la manera de estableces sus diagonales es siempre la misma.
Además de ser una figura muy popular en las matemáticas, también lo es fuera de este ámbito. Gracias a que posee un movimiento que la convierte en una figura más impactante que otras, como por ejemplo el cuadrado o el círculo. Muchas marcas y empresas han elegido al rombo como un logotipo o símbolos para sus productos. Algunos ejemplos son:
-La compañía japonesa Mitsubishi, posee un logo en el cual se aprecian tres rombos unidos por uno de sus vértices en el centro de la imagen, de manera tal que simulan tres partes de un gran triángulo.
-La compañía Renault, posee como logotipo un rombo al cual le han cortado dos secciones, tanto en la parte superior como en la inferior, dejándolo con dos vértices de más.
– En el juego de naipes, podemos encontrar a las cartas de diamantes, las cuales son rombos.
-Los barriletes, o también llamados cometas, suelen elaborarse con la misma forma geométrica de los rombos.
-La marca de ropa deportiva Umbro, ha optado como logo principal al rombo. A lo largo de los años ha ido modificando su logo pero siempre manteniendo al Rombo como logotipo principal.