Actualizado 26 enero, 2023
La multiplicación de fracciones es una de las operaciones matemáticas básicas que permitirán obtener una tercera fracción, la cual será el producto de las anteriores.
A continuación veremos como multiplicar fracciones con ejemplos y ejercicios.
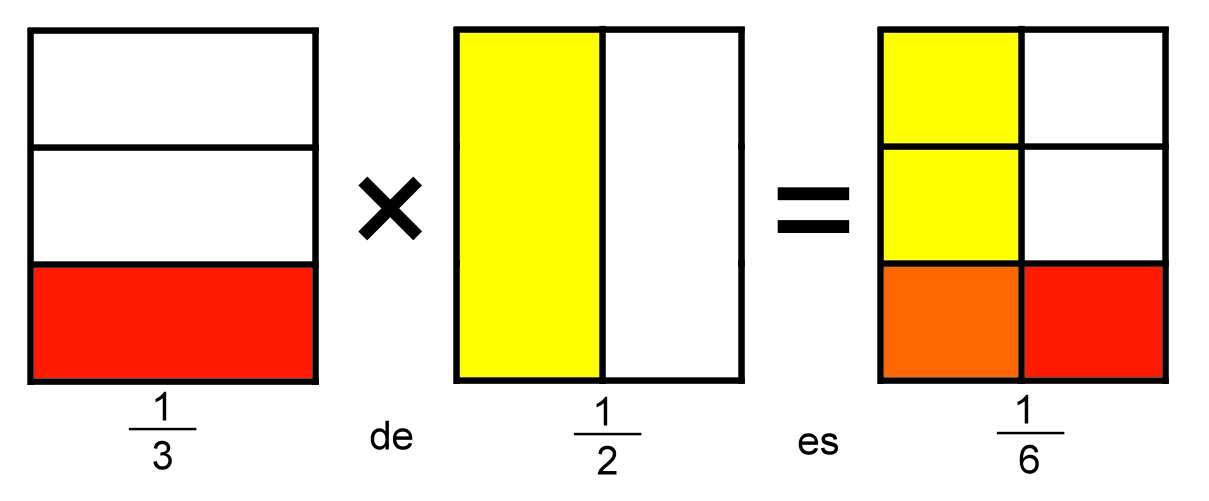
En términos matemáticos una fracción es un número que se obtiene de dividir un entero en partes iguales. Por ejemplo cuando decimos la quinta parte de una torta, estamos dividiendo la torta en cinco partes igual y solo consideramos una porción de ella (1/5).
Una fracción se representa gráfica y matemáticamente por números que están escritos uno sobre otros y separados por medio de una línea recta horizontal que se denomina raya fraccionaria. Los números que componen la parte superior reciben el nombre de numerador y los o el número que se encuentra en la parte inferior se llama denominador.
El numerador es la cantidad de partes que se consideran del total o de la unidad. En cambio el denominador es el número de partes iguales en que se haya dividido el total o la unidad.

Tipos de fracciones
Podemos encontrar distintos tipos de fracciones. Detallaremos a continuación cada una de ellas.
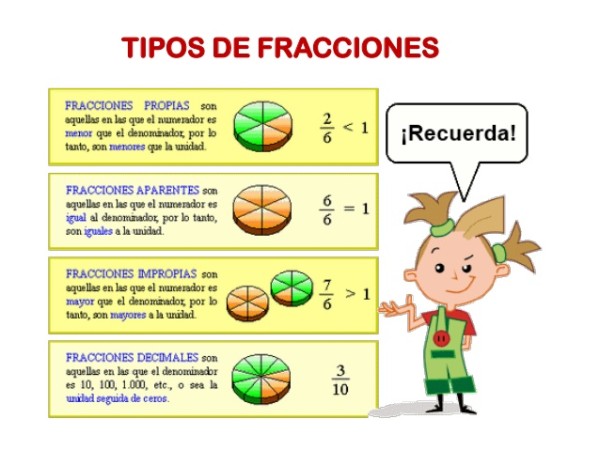
Fracción propia: Es aquella fracción en la que el numerador es menor que el denominador, esto significa que representa un numero mas chico que un entero. Algunos ejemplos: un quinto (1/5), tres octavos (3/8), un tercios (1/3).
Fracción impropia: son las fracciones en las cuales el numerador es mayor que el denominador, lo que implica que representa un número mas grande que el entero. Por ejemplo: ocho quintos (8/5), cuatro tercios (4/3).
Fracciones comunes y decimales: las fracciones comunes son aquellas cuyo denominador no es la unidad seguida de ceros. Por ejemplo: dos cuartos (2/4), un octavo (1/8). En cambio las fracciones decimales, son las que el denominador si es la unidad seguida de ceros. Por ejemplo: tres decimos (3/10), una centésima (1/100).
¿Cómo multiplicar fracciones?
Dentro de las operaciones matemáticas que podemos realizar con las fracciones, se encuentra la multiplicación. El símbolo que se utiliza para esta operación es la x (equis) o también puede representarse por medio de un punto (.) símbolo matemático al que se lo conoce como “por”.
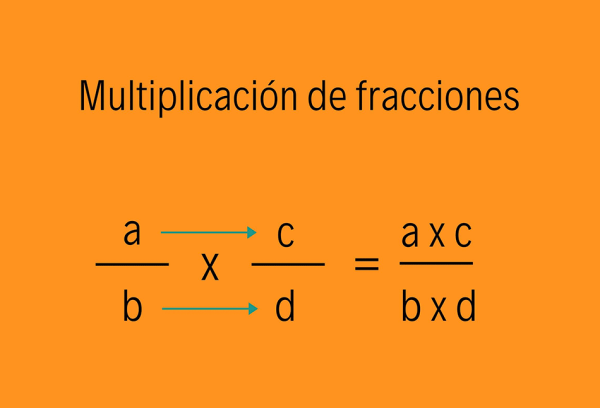
A diferencia de la suma de fracciones, para poder realizar multiplicaciones se utiliza un solo método. En este caso no importa si estamos frente a un caso de igual denominador o distintos denominador.
En las multiplicaciones de fracciones el procedimiento consiste en multiplicar los numeradores de las fracciones y por otro lado multiplicar los denominadores de las mismas. Por ejemplo: queremos realizar la multiplicación de las fracciones 1/2 x 2/2. Lo primero que haremos será multiplicar los numeradores (1 x 2) = 2, este resultado va en la parte superior. Luego hacemos el mismo procedimiento y ponemos el resultado en el denominador, de esta manera la respuesta a nuestro ejemplo es 2/4 (dos cuartos).
Veamos otro ejemplo: queremos multiplicar las fracciones 1/3 x 2/6, lo primero a realizar será multiplicar los numeradores de ambas fracciones (1 x 2) y colocamos el resultado en el numerado. Luego multiplicamos los denominadores de ambas fracciones (3 x 6) y colocamos el resultado en el denominador, de este modo obtendremos la respuesta a nuestra multiplicación de fracciones: 2/18.
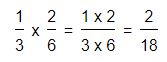
Ahora como vemos, el resultado que es 2/18 se puede simplificar ya que tanto el numerador como el denominador se puede reducir a la mitad. De esta forma luego de simplificarlo obtendremos como resultado la fracción de 1/9 (un noveno), ya la mitad de dos es uno y la mitad de dieciocho es nueve.
Luego de esto podremos decir que la fracción 2/18 y la fracción 1/9 son equivalentes, ya que representan la misma cantidad.
Multiplicación de más de dos fracciones
¿Cómo debemos proceder cuando queremos multiplicar más de dos fracciones? La respuesta a nuestra pregunta es que hay que proceder de la misma forma que hemos detallado anteriormente, esto es multiplicando en línea a los numeradores y luego multiplicando a los denominadores.
Por ejemplo: Queremos multiplicar las fracciones 4/2 x 5/3 x 3/2. Lo primero que haremos será multiplicar todo los numeradores y poner el resultado en el numerador: 4 x 5 x 3 = 60. Luego realizamos la misma operación pero con los denominadores: 2 x 3 x 2 =12. De esta manera tendremos como resultado la fracción 60/12, la cual verificamos que podemos simplificarla al dividir cada una de sus partes por seis: 60/6 es igual a 10 y 12 dividido seis es igual a 2. Resumiendo esta simplificación nos queda una fracción de 10/2 (diez medios), el cual al dividirlo nos arrojara como resultado cinco (5).
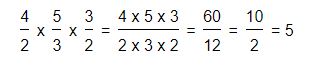
Multiplicación de fracciones por un número entero
Se puede dar el caso de tener que multiplicar una fracción por un número entero. En este caso lo primero que debemos hacer para poder resolverlo, será convertir el número entero en una fracción.
¿Cómo se convierte el numero entero en fracción? La respuesta a nuestra pregunta es muy simple: para poder realizar esto basta con poner un uno (1) como denominador del numero entero y realizando luego la multiplicación habitual de fracciones.
Ejemplo:
Queremos multiplicar la fracción 5/8 x el numero entero 3. Lo primero que debemos realizar será convertir el tres en una fracción, para esto le agregamos como denominador del mismo al numero uno, obteniendo de este modo una fracción que será de 3/1.
Una vez que logramos esto, solo basta con hacer la clásica multiplicación de las fracciones que es numerador por numerador y denominador por denominador.
En nuestro caso sería: 5/8 x 3/1. Multiplicamos cinco por tres y ocho por uno, obteniendo como resultado la fracción 15/8.
Multiplicación de fracciones mixtas
Para poder explicar el procedimiento para multiplicar fracciones mixtas, primero recordaremos cuales son. Las fracciones mixtas son aquellas que están compuestas por un numero entera y una parte fraccionaria, es decir son la suma de una parte entera más una fracción.

Para poder realizar multiplicaciones de fracciones mixtas es necesario poder expresar a la parte entera como una parte fraccionaria, para lograr de este modo que tenga el mismo denominador que la fracción que lo acompaña.
¿Cómo convertimos la parte entera en fraccionaria? Para lograr esto y poder realizar la multiplicación de las fracciones debemos:
- Multiplicar la parte entera por el denominador de la fracción que lo acompaña.
- Una vez que tenemos el resultado del paso anterior debemos sumarlo con el numerador de la fracción que lo acompaña.
- Por último, una vez convertidas las fracciones mixtas procedemos a realizar la multiplicación por el procedimiento habitual, esto es multiplicamos numerador por numerador y denominador por denominador.
Veamos un ejemplo para entenderlo de manera correcta
-Suponiendo que tenemos la siguiente fracción para multiplicar:
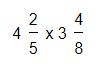
Lo primero que vamos a realizar será la conversión de la fracción mixta, para esto vamos a multiplicar el número entero (4) por el denominador de la fracción que lo acompaña:
4 x 5 = 20
Lo mismo realizaremos con la otra fracción mixta, multiplicamos el número entero que es tres por el denominador de la parte fraccionaria que es ocho:
3 x 8 = 24
Una vez que obtenemos dichos resultados, pasaremos a la etapa siguiente que es sumarlo con el numerador de las fracciones que los acompañan. En este ejemplo serian:
20 + 2 = 22
24 + 4= 28
De esta manera con estos resultados ya tenemos convertidas las fracciones mixtas y podremos resolver la multiplicación de manera tradicional. Las nuevas fracciones que tenemos son:
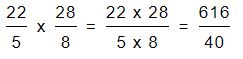
Una vez multiplicado el numerador por el numerador y el denominador por el denominador obtendremos el resultado de nuestra multiplicación de fracciones mixtas que es 616/40.
Ejercicios para practicar
A continuación dejaremos algunos ejercicios para que puedan practicar y entender bien la multiplicación de fracciones.
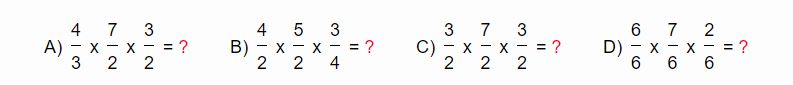
Resoluciones de los casos anteriores
