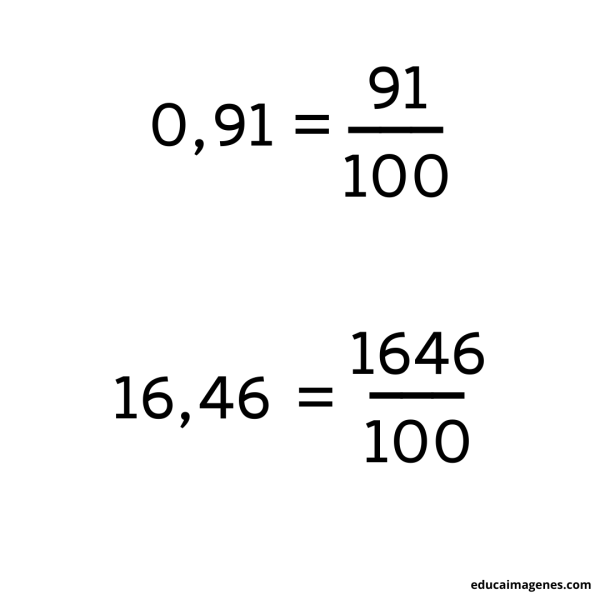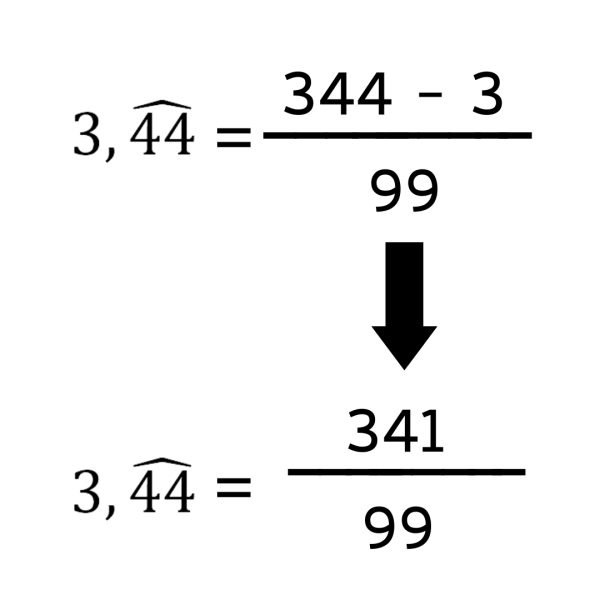Actualizado 9 septiembre, 2022
Si estás estudiando sobre como convertir fracciones a decimales y números decimales en fracciones, pero aún no comprendes, te traemos la información necesaria para que puedas entender el tema en cuestión. Seguidamente, encontrarás la explicación de como pasar decimales a fracciones y fracciones a decimales, además te brindaremos ejemplos y ejercicios para que practiques.
Convertir decimales a fracciones
A continuación te mostraremos el paso a paso para convertir decimales a fracciones. Pero primero veremos cuales son los tipos de números decimales.
Números decimales exactos
Son aquellos que tienen cifras decimales limitadas, que tienen un número finito.
Números decimales periódicos puros
Son aquellos que poseen cifras decimales infinitas, estas siguen un patrón, llamado periodo. Sobre el periodo se coloca un arco.
Se los llama puros porque su parte periódica comienza después de la coma.
Números decimales periódicos mixtos
Los números decimales periódicos mixtos se asemejan a los puros en la cuanto a que contienen números periódicos. Pero la diferencia radica en que antes del periodo se hallan cifras decimales, esto se llama anteperiodo.
Números decimales infinitos no periódicos
En este caso, los números decimales infinitos no periódicos poseen números infinitos, pero los mismos no tienen un patrón.
Una vez comprendidos los distintos tipos de números decimales, veremos como convertir los mismos en fracciones.
Para pasar un numero decimal exacto a fracción debemos ubicar en el numerador el número decimal «entero» quitándole la coma, y en el denominador debemos poner 1 (uno) más un 0 (cero) por la cantidad de números que haya después de la coma.
Por ejemplo: si tenemos 0,91, debemos colocar en el numerador el número 91 y en su denominador un 1 más dos 0 (ceros) debido a que hay dos números después de la coma.
Cuando el número decimal es periódico puro para pasarlo a fracción debemos colocar en el numerador el número completo, es decir, la parte entera junto con el periodo y a este número debemos restarle la parte entera. En la parte del denominador debemos escribir tantos nueves como cifras tenga el periodo.
Por ejemplo: si tenemos el número 3,44 periódico, pondremos 344 en el numerador y le restaremos 3, dando como resultado 341. Y en su denominador escribiremos dos 9 ya que hay dos números en el periodo.
En el caso del número decimal periódico mixto para convertirlo en fracción colocaremos en el numerador la parte entera junto con el anteperiodo y el periodo, y a este número le debemos restar la parte entera junto con el anteperiodo. Y como denominador, se pondrán tantos nueves como cifras contenga el periodo y seguidamente, se escribirán tantos ceros como cifras tenga el anteperiodo.
Por ejemplo: en el número 1,98(313)periodo, en el numerador pondremos 198313 y le restaremos 198, dejando como número final 198115, y en su denominador pondremos tres 9 porque esta es la cantidad que contiene el periodo y colocaremos dos 0 (ceros) ya que su anteperiodo posee dos números.
Los números decimales infinitos no periódicos o racionales son los únicos que no se pueden convertir en fracción.
Ejemplos para encontrar fracciones equivalentes
Las fracciones equivalentes son aquellas que representan la misma cantidad con diferentes números en su numerador y en su denominador. Aquí debajo encontrarás distintos ejemplos que te ayudarán a encontrar fracciones equivalentes.
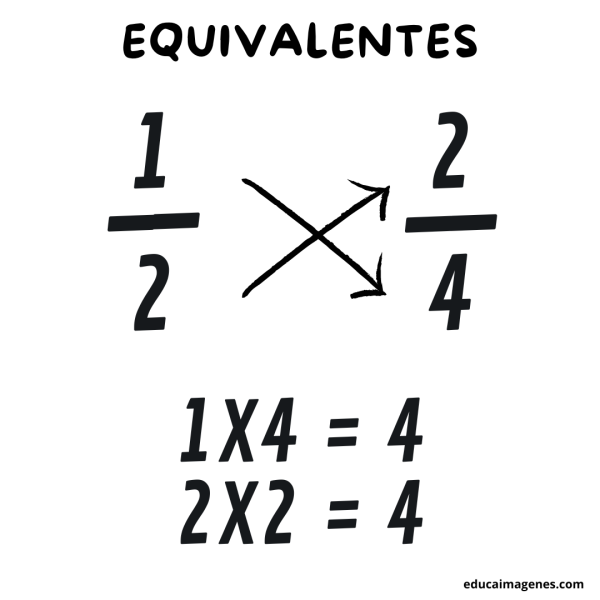
Para comprobar si las fracciones son equivalentes debemos multiplicar de manera cruzada, es decir, numerador con denominador y denominador con numerador. Si ambas multiplicaciones nos dan como resultado el mismo número, podemos dar por hecho que ambas fracciones son equivalentes.
Por ejemplo: si multiplicamos la fracción 1/2 por la fracción 2/4 de manera cruzada, el resultado de estos cálculos es 4 en ambos casos, por lo tanto son fracciones equivalentes.
Por otro lado, en el siguiente ejemplo, si multiplicamos 1/2 por 3/4 de manera cruzada, obtendremos dos resultados distintos, lo que indica que las fracciones no son equivalentes.
Para encontrar fracciones equivalentes podremos realizar los siguientes cálculos:
Amplificación
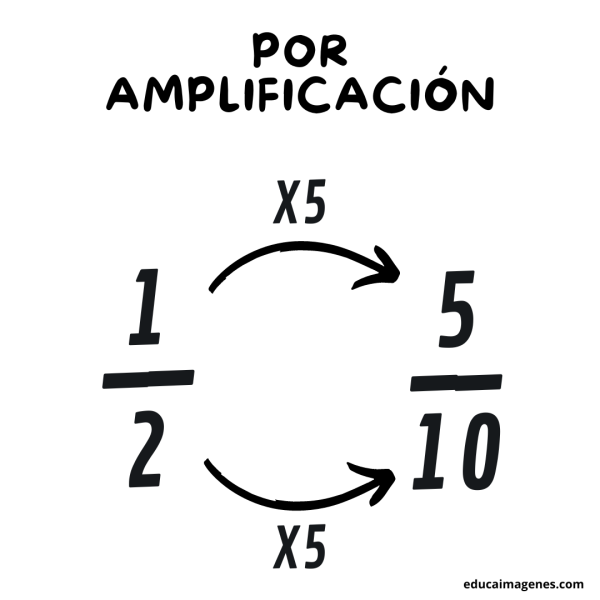
Para hallar una fracción equivalente por amplificación, debemos multiplicar tanto denominador como numerador por el mismo número.
Por ejemplo: multiplicamos por 5 tanto el numerador, siendo este 1, como el denominador, que es 2.
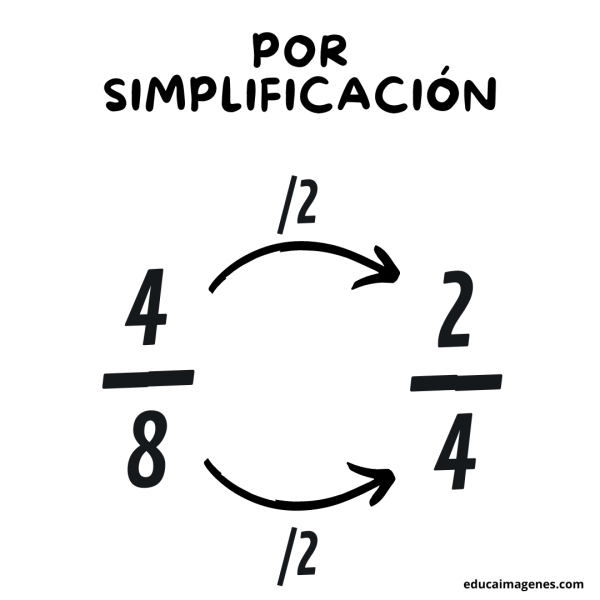
Simplificación
Para utilizar la simplificación como herramienta para encontrar fracciones equivalentes, se debe dividir el numerador y el denominador por un divisor común a ambos números.
Por ejemplo: debemos dividir el 4 y el 8 por el 2, ya que este último es divisor de ambos números.
Ejercicios para pasar decimales a fracciones
Luego de realizar las explicaciones necesarias, te dejamos aquí debajo ejercicios para pasar decimales a fracciones. Realízalos para poder aplicar los conocimientos obtenidos.
Pasar una fracción a número decimal
Ahora, por el contrario a todos los ejercicios planteados anteriormente, expondremos como se pasa una fracción a un número decimal. Aquí encontrarás la información que necesitas para aprender a realizarlo.
Comencemos definiendo que es una fracción, la misma es un número que representa las partes de un todo, es decir, es un todo que se ha divido en partes. Por ejemplo, si tenemos una pizza y la dividimos en 8 porciones, obtendremos la fracción 1/8. Asimismo, una fracción también puede representar una parte de un grupo, por ejemplo, si tenemos 6 manzanas y nos comemos dos, tendremos la fracción 2/6.
La fracción se compone de dos partes, por un lado, el número que se ubica por encima de la línea media, se llama numerador y nos indica cuantas partes del conjunto se toman. Y el número que se encuentra por debajo de la línea se llama denominador, el cual nos indica en cuantas partes fue repartida la unidad.
Las fracciones se pueden clasificar en:
Fracciones unitarias
Se llaman fracciones unitarias aquellas que su numerador sea 1 (uno).
Fracciones propias
Las fracciones propias son aquellas en las que el denominador es mayor que el numerador.
Fracciones impropias
Cuando hablamos de fracciones impropias nos referimos a las fracciones que tienen un número igual o mayor en su numerador que en el denominador.
Fracciones mixtas
Por último, las fracciones mixtas constan de un número entero junto con una fracción propia.
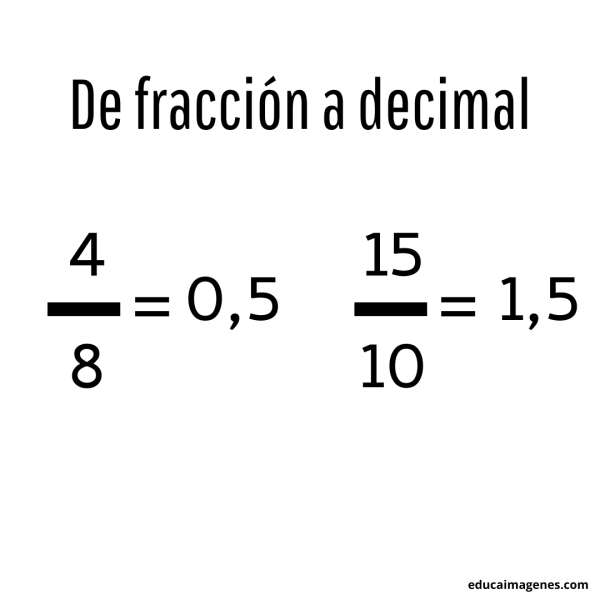
Para convertir una fracción en un número decimal debemos hacer lo siguiente, solo debemos dividir el numerador por el denominador.
Por ejemplo: si tomamos la fracción 4/8, al realizar la división de 4 por 8 obtendremos como resultado 0,5.
Sin embargo, si tenemos una fracción mixta, la cual se compone por un número entero y por una fracción. Primero debemos realizar lo mismo que en la fracción simple, tomamos la fracción y dividimos su numerador por su denominador. Una vez obtenido este resultado, debemos sumarle el numero entero delante.
Por ejemplo: si nuestra fracción es 2 3/6, primero dividiremos 3 por 6, lo cual nos da 0,5, y al sumarle el número entero nos da un resultado de 2,5.
Respecto a los resultados que nos pueden dar las conversiones de fracciones a números decimales encontramos los siguientes:
De fracción a número decimal exacto
Para obtener un número decimal exacto debemos dividir el numerador por el denominador y nos debe dar como resultado un número de decimales limitado.
De fracción a número decimal periódico puro
La conversión de una fracción a número decimal periódico puro, se debe dar cuando al dividir el numerador por el denominador alcanzamos como resultado un número que no posee decimales limitados y se repite en forma de patrón.
De fracción a números decimales periódicos mixtos
Al dividir el numerador por su denominador el resultado con el que nos toparemos será un número en el cual se repiten los decimales periódicamente pero no justo luego de la coma.
Ejercicios para convertir fracciones a números decimales
Para afianzar la información brindada te traemos distintos ejercicios para convertir fracciones a números decimales. Intenta resolverlos todos, para verificar si has comprendido bien el tema.
Deseamos que toda la información compartida haya sido de tu ayuda, deseamos que puedas comprender el tema y practiques todo lo necesario para dominar la conversión de fracciones y de números decimales. Esperamos tus sugerencias o dudas en los comentarios.