Actualizado 16 marzo, 2021
Los números decimales son valores que representan números que son más pequeños que la unidad, es decir números racionales e irracionales. Estos números a diferencia de los fraccionarios no se escriben como el cociente entre dos números enteros, sino que se escriben como una aproximación de tal valor.
Los números decimales suelen ser difíciles de imaginar y de representar mentalmente, por eso es común que los mismos sean dimensionados como fracciones, es decir como unidades enteras divididas. Por eso en el día de hoy aprenderemos como convertir estos números decimales en fracciones.
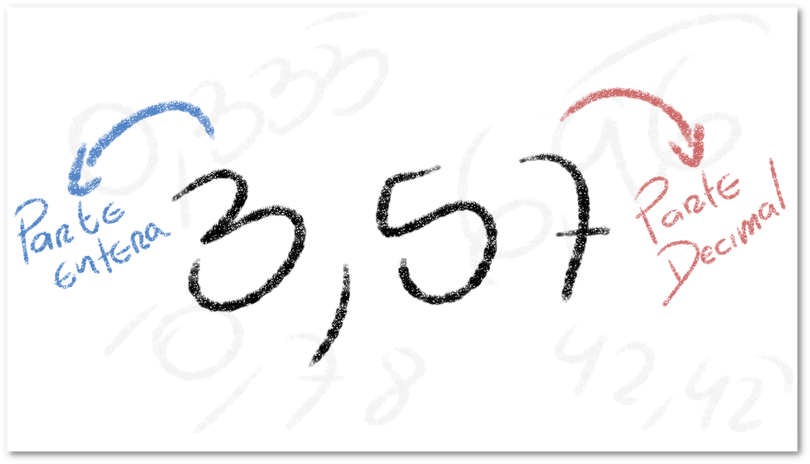
¿Qué son los números decimales?
Un numero decimal es la expresión de un numero que no es entero y que tiene una parte decimal. Esto quiere decir que cada número decimal se compone por una parte entera y una parte decimal que va separada por una coma. Los números decimales son una de las maneras que existen para describir a las fracciones que tienen como resultado un cociente inexacto.
Los números decimales son los valores que representan a aquellos números que son más pequeños que la unidad. Podemos decir que un número decimal es un valor aproximado que permite expresar un número racional e irracional en un valor aproximado. Estos números se componen por una parte entera que se encuentra a la izquierda del punto o la coma decimal y una parte decimal que se encuentra a la derecha. Si tenemos el caso de que un número decimal no tenga una parte entera, se procederá a escribir un cero al lado izquierdo o delante de la coma.
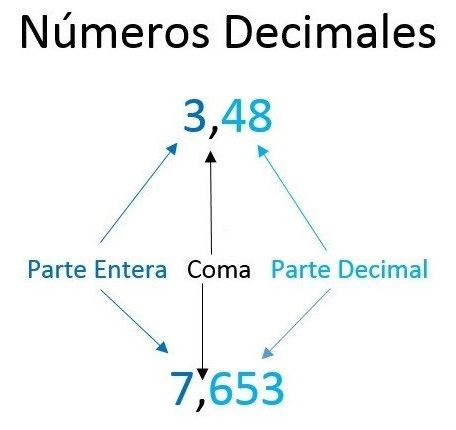
Veamos un par de ejemplo para comprender los números decimales:
8,654
Tal como podemos ver el número entero que encontramos primero es el ocho, el cual se ubica por delante de la coma. Por otro lado después de la coma encontramos al número decimal que en este caso consta de tres cifras y es 654.
0,23
Aquí vemos otro ejemplo de número decimal, en el cual la parte entera se reduce a cero, por lo tanto se considera que la parte entera es nula. Por otro lado la parte decimal consta solo de dos cifras.
Clasificación de los números decimales
Existen diferentes formas de separar a los números decimales, puede ser con una coma, con un punto, con un apostrofe, esto lo decide quien lo escribe. Dependiendo de cada resultado que den los números decimales, los mismos se podrán clasificar en:
–Números decimales exactos: son aquellos que posee una cantidad de números de decimales específicos (limitados) o que tienen una cifra final en la parte decimal. Estos números se pueden escribir sin requerir de una gran esfuerzo. Ejemplos:
0.8
2.6563
13.5843
148.54
–Números decimales periódicos: Son aquellos que tienen un numero ilimitado o infinitos de cidras decimales, pero que se repiten en un patrón o periodo especifico que es notable dentro de un numero de cifras variables en cada caso. Se trata de un numero infinito, que no puede ser escrito indefinidamente, y es por esta razón que se utilizan los tres puntos seguidos que representan la infinidad. Ejemplos:
1,33333333…
6,05050505…
13,18181818…

Dentro de esta clasificación de números decimales periódicos encontramos otra clasificación que los divide en puros y en mixtos.
Los números decimales periódicos puros son aquellos en donde los decimales son parte del mismo grupo, es decir que existe un periodo o patrón desde la primera cifra decimal, por ejemplo:
3,555555…
15,123123…
Los números periódicos mixtos son aquellos en donde existen cifras que se encuentran fuera del patrón o periodo de cifras decimales, es decir las primeras cifras decimales no presentan un patrón o periodo pero luego algunas cifras empieza a mostrar un periodo, por ejemplo:
9,366666…
23,62222…
–Números decimales no periódicos: son aquellos que poseen cifras decimales infinitas que no pueden ser definidas como un patrón definido. Son números irracionales tales como el número pi, la raíz cuadrada de dos, entre otros.
Ejemplo: el conocido numero pi, representa el cociente entre la longitud de la circunferencia y la longitud de su diámetro. La aproximación de este número es 3.141592653589…
Composición de un numero decimal
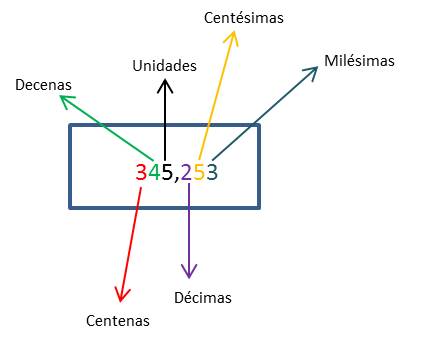
Los números decimales están compuestos de cifras que son separadas de la parte entera por medio de una coma, de un punto, de un apostrofe. Según la posición en la que se ubiquen estas cifras tienen características que las diferencias. Si las decimas se ubican luego de la coma o del separador indica que las centésimas están dos lugares después de la coma, las milésimas en el tercer lugar y así sucesivamente. Vemos un ejemplo:
Si tenemos el numero 7,851 podemos ver que la parte entera es el 7, la decima es el 8, la centésima es el 5 y la milésima es el 1.
¿Cuál es la relación de los decimales con las fracciones?
La relación que encontramos entre los decimales y las fracciones es:
La Unidad se representa por 1
La Décima es la unidad dividida en 10 partes iguales = 1/10 = 0,1
La Centésima es la unidad dividida en 100 partes iguales = 1/100 = 0,01
La Milésima es la unidad dividida en 1000 partes iguales = 1/1000 = 0,001

¿Cómo convertir un decimal en una fracción?
Para poder convertir un número decimal en una fracción se deberán seguir los siguientes pasos:
- Lo primero a realizar será expresar el número decimal en forma de fracción. Para esto sabemos que cualquier numero dividido entre uno da como resultado el mismo numero. En forma de fracción lo expresaríamos de la siguiente manera:
Por ejemplo tenemos el número 0,35 y para convertirlo en fracción lo dividimos por uno quedándonos: 0,35 / 1
- En el paso número dos debemos contar los números a la derecha del punto o la coma decimal y multiplicarlos por diez elevado a la cantidad de números. Es muy importante multiplicar el numerador y el denominador para que de este modo no se altere el valor de la fracción. El resultado que obtendremos sera el numero decimal convertido en fracción. Por ejemplo, si tenemos dos numero luego de la coma, los multiplicamos por 100, si tenemos tres números los multiplicamos por 1000 y así sucesivamente.
- El paso numero tres será simplificar o reducir la fracción. Este paso podría ser descartado. Simplificar seria encontrar una fracción equivalente.
Ejercicios para convertir decimales en fracciones
A continuación veremos algunos ejercicios para entender como se hace esta conversión.
-Ejemplo numero 1:
Queremos expresar el numero decimal 0,75 como una fracción. Por lo tanto lo primero que haremos será escribir el número como una fracción:
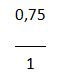
Una vez que tenemos este número, seguiremos por multiplicar el numero de abajo y el de arriba por 100 ya que como vemos hay dos dígitos luego de la coma:
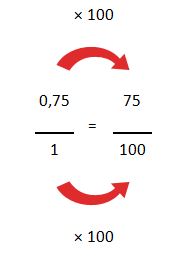
Por ultimo tendremos que simplificar la fracción en caso que sea posible: De este modo ya podemos observar como el número de arriba se convierte en un número entero.
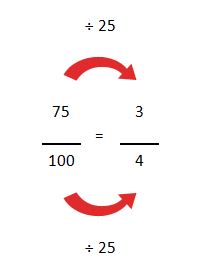
Como resultado obtendremos a la fracción ¾.
-Ejemplo número 2:
Queremos expresar el numero decimal 0,333 como una fracción. Por lo tanto lo primero que haremos será escribir el número como una fracción:
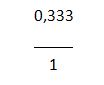
De este modo ya podemos observar como el número de arriba se convierte en un número entero. Una vez que tenemos este número, seguiremos por multiplicar el número de abajo y el de arriba por 1000 ya que como vemos hay tres dígitos luego de la coma:
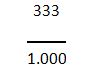
Por ultimo tendremos que simplificar la fracción en caso que sea posible y como vemos en este ejercicio no podemos realizar la reducción de la fracción, por lo tanto el resultado será 333/1000.
A continuación te dejamos unos ejercicios para que practiques la conversión de decimales en fracciones:
a) 0,24=………
b) 1.75=………
c) 7,04=………
d) 5,9=………