Actualizado 11 diciembre, 2020
Una fracción expresa una división, es decir que representa un reparto o una porción de una unidad. Las fracciones son elementos de las matemáticas que representan una proporción determinada entre dos cifras.
Las fracciones mixtas son las combinaciones entre un número entero y una fracción. A continuación conoceremos más acerca de este tipo de fracciones.

¿Qué son las fracciones?
Las fracciones se pueden definir como elementos de las matemáticas que representan la proporción entre dos cifras. Son la representación de las partes de un todo, esto quiere decir que si dividimos algo en parte iguales y tomamos uno de estas partes la forma que tenemos de expresarlo es por medio de las fracciones. Al tratarse de un cociente, las mismas se pueden expresar tal como su resultado, esto quiere decir un número único ya sea entero o decimal, de este modo todas las fracciones pueden ser reexpresadas como números.
La forma de escribir las fracciones grafica y matemáticamente es a través de los números, los cuales se expresan uno por encima del otro y separador por medio de una línea horizontal o también denominada raya fraccionaria. Los números que se encuentra por encima de la raya fraccionaria se denominan numeradores, por el contrario los números que se encuentran debajo de la raya se denominan denominadores. Este ultimo actúa como divisor.
Veamos un ejemplo: supongamos que tenemos la fracción 5/8, esta significa que 5 es dividido por 8, como resultado obtendremos 0.652.
En el caso en que el denominador sea menor que el numerador obtendremos que la fracción es mayor que la unida, por lo tanto la misma podrá ser reexpresada como un numero entero más una fracción menor que uno.
Es normal que las fracciones se expresen con las cifras más pequeñas que se pueda, para lograr esto es necesario buscar el denominador entero más pequeño que haga que el numerador también sea un numero entero. Por ejemplo mirando el ejemplo anterior, la fracción 8/5 no tiene forma de ser más pequeña ya que no existe ningún numero entero menor que ocho que a la vez sea también divisor de cinco.
¿Qué es una fracción mixta?
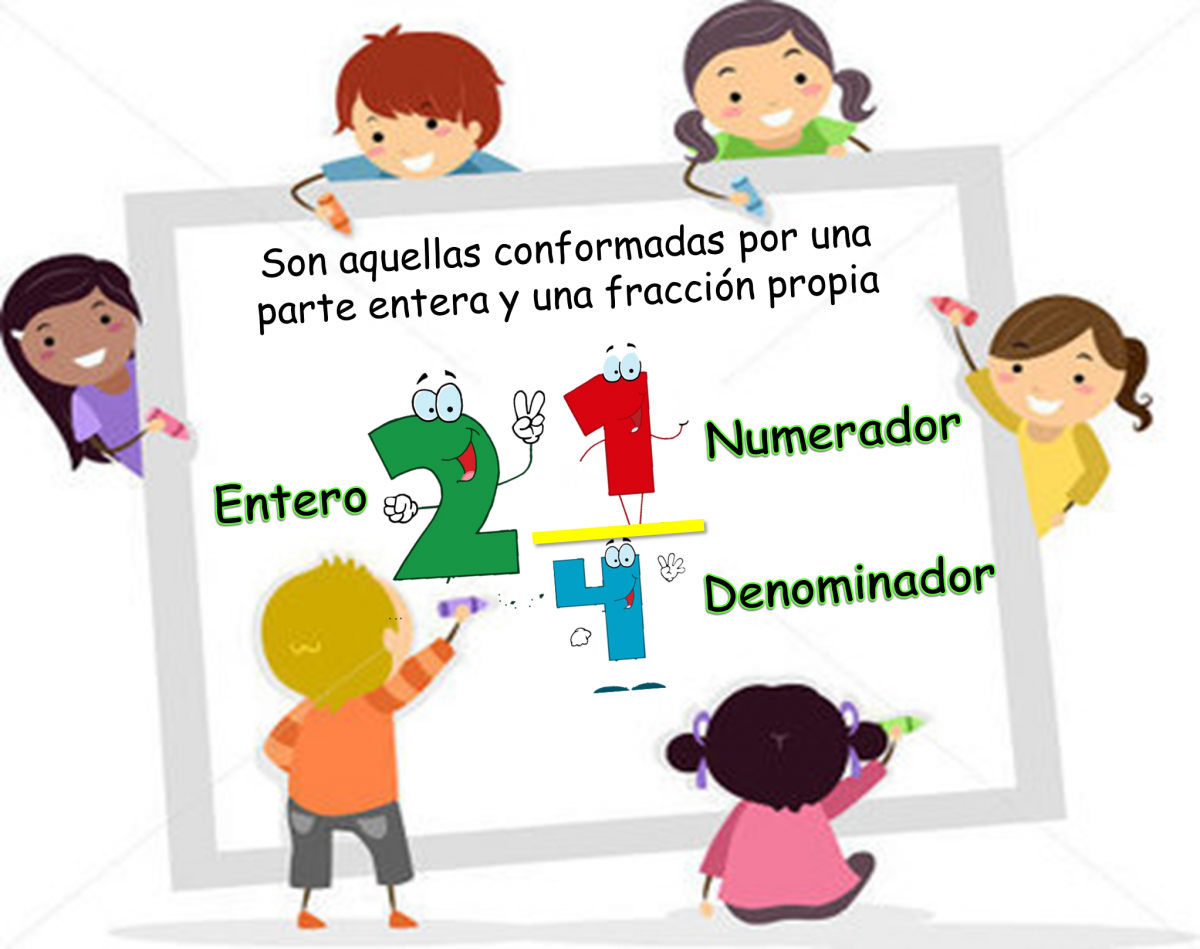
Existen distintos tipos de fracciones, entre ellos podemos encontrar a las fracciones mixtas. Las mismas son aquellas fracciones que poseen una combinación de un número entero y una fracción. Un claro ejemplo de fracción mixta sería 2 3/4, la correcta forma de denominarlo sería: dos enteros y tres cuartos.
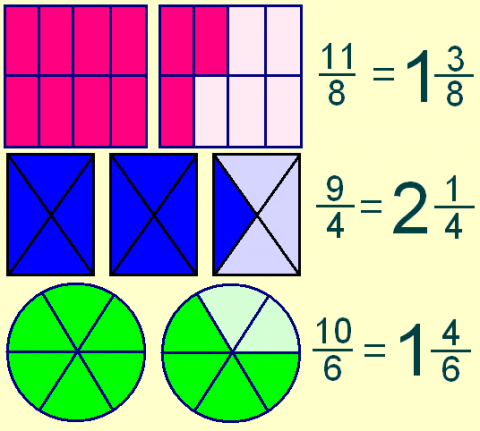
Tal como indicábamos anteriormente el número que se encuentra por arriba de la raya fraccionaria, llamado numerador, es el número de partes tomadas de la unidad. Por ejemplo si un individuo toma dos porciones de pizza, esta tomando 2/8. En este caso el numerador es dos.
El denominador es el número de partes que integran la totalidad de la unidad. En el ejemplo anterior seria el total de partes en que se divide la pizza (ocho).
En aquellos casos en que el numerador es mayor que el denominador estamos frente a un caso donde existe más de una unidad completa. En estos casos la cantidad puede expresarse por medio de una fracción impropia (donde el numerador es mayor que el denominador) o sino por medio de una fracción mixta. De lo contrario una fracción propia nunca podrá expresarse como una fracción mixta.
¿Cómo convertir fracciones impropias en fracciones mixtas?
Para poder convertir fracciones impropias en fracciones mixtas, debemos:
-Dividir el numerador por el denominador.
-Escribir el cociente como número entero.
-El resto será el nuevo numerador de la fracción (siempre con el mismo denominador).
¿Cómo convertir fracciones mixtas en fracciones impropias?
-Multiplicar el número entero por el denominador.
-Sumar el resultado al numerador.
-El resultado de la suma será el nuevo numerador de la fracción (siempre con el mismo denominador).
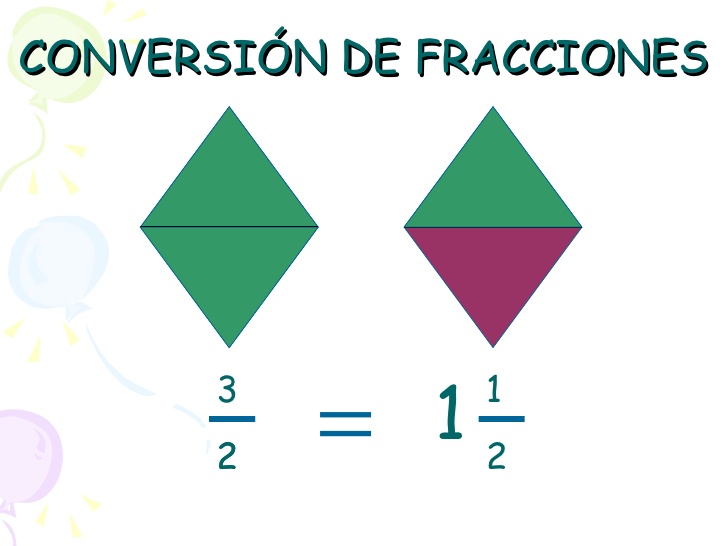
¿Cuándo se utilizan las fracciones mixtas?
Es muy común el uso de las fracciones mixtas en la vida cotidiana, por ejemplo la gente suele decir: me comí 2 ½ empanadas o voy a comprar 2 ½ de manzanas. Sin embargo en matemáticas son mejores las fracciones impropias que las mixtas, ya que estas últimas suelen confundirse cuando se las escribe en una formula.
Ejemplos de fracciones mixtas
3 3/5 (tres enteros y tres quintos)
1 2/4 (Un entero y 2 cuartos)
45 74/100 (cuarenta y cinco enteros y setenta y cuatro centésimos)
62 3/9 (sesenta y dos enteros y tres novenos)
2 5/7 = (Dos enteros y cinco septimos).
5 4/7 = (Cinco enteros y cuatro séptimos).
8 3/10 = (Ocho enteros y tres décimos).
11 2/5 = (Once quintos y dos quintos).
7 4/10 = (Siete enteros y cuatro décimos).
265 10/14 = (Doscientos sesenta y cinco enteros y diez catorceavos).
Operaciones con fracciones mixtas
Según el tipo de problemas se puede representar una fracción como mixta o impropia, pero para esto primero se debe tener bien en claro los conceptos para poder convertir fracciones mixtas en impropias o viceversa.
Repasando lo que hemos comentado anteriormente, sabemos que una fracción impropia es aquella en la que su denominador es mayor que el denominador.
En los casos en que un número sea expresado con entero y decimales, lo primero a realizar será convertir la parte decimal en fracción.
Cuando tengamos operaciones con fracciones mixtas, primero debemos convertir estas fracciones en una fracción impropia.
Suma de fracciones mixtas
Para resolver las sumas de fracciones mixtas primeros debemos cumplir con los siguientes pasos:
-Convertir las fracciones mixtas a impropias.
-Realizar la operación correspondiente para resolver la suma de fracciones.
Cuando estamos frente a una suma de fracciones mixtas, siempre será necesario que la parte entera se exprese como una fracción del mismo denominador que en la parte fraccionaria que lo acompaña. Veamos un ejemplo:
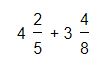
Lo primero a realizar será multiplicar la parte entera por el denominador de la fracción. De este modo obtendremos:
5 x 4= 20
3 x 8= 24
Luego sumamos el resultado de la multiplicación con el denominador de la fracción y el resultado ira en el numerador de cada fracción:
20 + 2= 22/5
24 + 4= 28/4
De esta manera convertimos las fracciones y ya podemos realizar la suma:
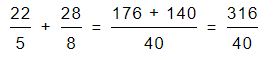
Resta de fracciones mixtas
Al igual que para las sumas, cuando tenemos que resolver las restas de fracciones mixtas primeros debemos cumplir con los siguientes pasos:
-Convertir las fracciones mixtas a impropias.
-Realizar la operación correspondiente para resolver la resta de fracciones.
Cuando tenemos resta de fracciones mixtas, siempre será necesario expresar la parte entera como una fracción con igual denominador que en la parte fraccionaria que a esta acompaña. Veamos un ejemplo:
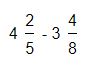
Lo primero a realizar será multiplicar la parte entera por el denominador de la fracción que la acompaña, de este modo obtendremos:
5 x 4= 20
3 x 8= 24
Luego se suman estos resultados con el numerador de la fracción. El denominador sigue siendo el mismo:
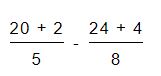
Por último, una vez convertidas las fracciones mixtas ya podemos realizar la resta por el método tradicional.
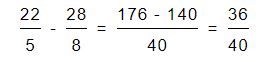
Multiplicación de fracciones mixtas
La multiplicación de fracciones es una de las operaciones que permite obtener como resultado una tercera fracción la cual será el producto de las anteriores y la que recibirá el nombre de resultado de la multiplicación.
Para poder obtener el valor numérico en forma de fracciones, existe un solo procedimiento tanto si las fracciones tienen igual denominador como si tienen distintos denominador. En el caso de las operaciones de multiplicación de fracciones se multiplican los numeradores de las fracciones y aparte los denominadores. Ejemplo:
Teniendo para multiplicar las fracciones 1/3 x 2/6, se procede a multiplicar denominador por denominador (1 x 3) y numerador por numerador (3 x 6). De este modo obtendremos el resultado de 2/18.
Este resultado a su vez se puede simplificar, ya que tanto el denominador como el numerador se pueden reducir a la mitad. Por lo tanto el resultado de nuestra operación será 1/9.
Ejercicios de operaciones con fracciones mixtas
A continuación dejamos algunos ejercicios con sus respectivas respuestas para que puedan poner en práctica las operaciones de las fracciones mixtas:

