Actualizado 4 mayo, 2021
Las fracciones son una representación de las partes de un todo, esto quiere decir que si dividimos algo en partes iguales y seleccionamos una de esas partes, podremos representarlo por medio de una fracción. A continuación aprenderemos a representar las fracciones.

¿Qué es una fracción?
Una fracción es la representación de las partes de un todo, esto significa que si se divide algo en partes iguales, cada una de esas partes será una fracción del entero. Por ejemplo: si tenemos una torta que esta divida en ocho partes iguales, cada una de las porciones equivale a un octavo (1/8) del total y si uno de los invitados se come 3 porciones, podemos decir que se comió 3/8 (tres octavos) de la torta.
Las fracciones se pueden definir como elementos de las ciencias matemáticas que representan una proporción entre dos cifras. Al tratarse de un cociente, las mismas se pueden expresar tal como su resultado, esto significa que se podrá expresar un número único ya sea entero o bien decimal. De esta forma todas las fracciones pueden ser reexpresadas como números.
Una fracción se compone de dos términos, un numerador y un denominador. Se llama numerador al término superior de la fracción y es el número que se encuentre por encima de la raya fraccionaria, el mismo indica el número de partes que se considera de la unidad o del total. Por otro lado esta el denominador que es el termino inferior y se encuentra por debajo de la raya fraccionaria. Este ultimo indica el numero de partes iguales en las que se ha divido la unidad o el total. Tal como indicábamos, el numerador y el denominador están separados por una raya fraccionaria o también denominada barra oblicua u horizontal.
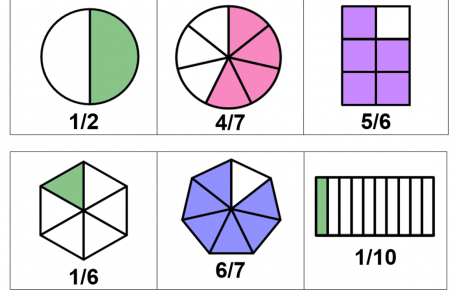
Veamos un ejemplo: Si tenemos la fracción 4/7, vemos que la misma representa 4 divido 8 y esto equivale a: 0.571. En este ejemplo el numerador es menor que el denominador por lo tanto el valor del cociente será menos a uno. De lo contrario si el numerador es mayor que el denominador implica que la fracción es mayor que la unidad, y por ende podrá ser reexpresada como un valor entero más una fracción menor de 1.
Otro concepto a tener cuenta es que el mismo número puede ser reexpresado por una cantidad infinita de fracciones, por ejemplo si miramos la fracción 5/8, la misma será igual a las fracciones 10/16, a 15/24 y a 5000/8000, las cuales siempre serán equivalentes a un mismo resultado (en este ejemplo 0,625). Estas fracciones reciben el nombre de equivalentes y siempre mantienen una relación de proporcionalidad directa.
¿Cómo se leen las fracciones?
Cada una de las fracciones tendrá un nombre específico y se podrán leer como tal, según el numerador y el denominador que tengan.
El número que se encuentra en el numerador se lee de igual manera, pero no ocurre lo mismo con el número que se encuentra en el denominador. Cuando el denominador va de dos a diez, tendrá un nombre específico:
-Si es 2 es «medios»
-Si es 3 es «tercios»
-Si es 4 es «cuartos»
-Si es 5 es «quintos»
-Si es 6 es «sextos»
-Si es 7 es «séptimos»
-Si es 8 es «octavos»
-Si es 9 es «novenos»
-Si es 10 es «décimos»
-Si el numero es mayor a diez se le agregará al numero la terminación sin «avos«.
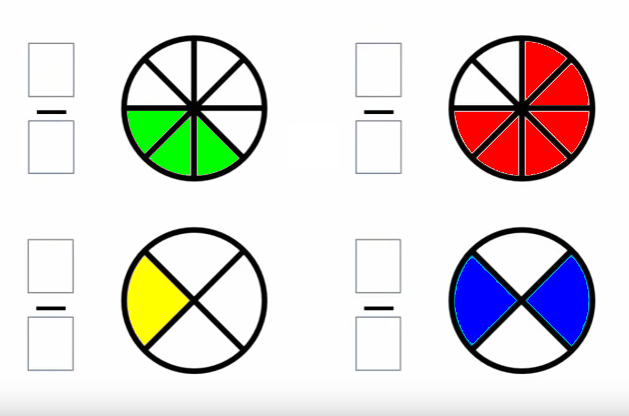
¿Cómo representar las fracciones?
La forma de representar las fracciones es por medio de una separación de los dos números con una raya fraccionaria o bien línea horizontal. En la parte superior se expresa al numerador y en la inferior al denominador. Otra de las formas de representar gráficamente las fracciones es por medio de figuras geométricas. A continuación detallamos como se realiza:
-Fracciones propias
En el caso de las fracciones propias (aquella en que el numerador es menor que el denominador), lo primero a realizar será elegir una figura geométrica: circulo, rectángulo, cuadrado, entre otras. Luego la dividimos en partes iguales, el total de partes en que se divida el dibujo dependerá del denominador, ya que el mismo indica en cuantas partes se divide la unidad.
Una vez realizado esto, marcaremos en el grafico las partes que indica el numerador (que es el número que esta por encima de la raya fraccionaria y el que indica cuantas partes se tomarán del total).
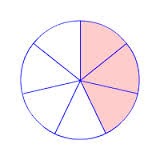
Por ejemplo: Queremos representar gráficamente la fracción 3/7. Para esto elegimos la figura geométrica, en este caso un círculo el cual dividimos en siete partes iguales, tal como indica el denominador. Luego marcaremos tres de las siete partes (tal como indica el numerador).
-Fracciones impropias
En el caso de las fracciones impropias, que son aquellas en donde el numerador es mayor que el denominador y el resultado de la fracción es mayor que uno, debemos utilizar más de una unidad o figura geométrica para representarla.
Del mismo modo que en las fracciones propias, lo primero que haremos será elegir la figura geométrica que queramos para hacer la representación, luego la dividimos en tantas partes iguales como indica el denominador de la fracción. En este tipo de fracciones veremos que como el numerador es mayor que el denominador, no podremos marcar todas las partes que indique su numerador, por lo tanto tendremos que utilizar una segunda figura geométrica y volver a dividirla en las mismas partes iguales y en ella marcar las partes que nos faltaban.
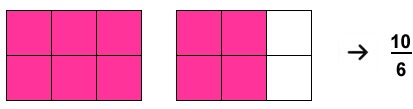
Por ejemplo: Queremos representar la fracción de 10/6, lo primero que haremos será elegir la figura geométrica que utilizaremos en la representación. En este ejemplo seleccionamos un rectángulo, al cual dividimos en seis partes iguales tal como indica el denominador de la fracción a representar.
Luego veremos que el numerador es diez, y como el rectángulo posee solo seis partes nos estarían faltando cuatro más, por lo tanto dibujamos otro rectángulo también dividido en seis partes como indica el denominador. En este nuevo dibujo seleccionaremos las cuatro partes que nos faltan para completar las cantidades que indica el numerador de la fracción.
De este modo, para poder representar nuestra fracción necesitaremos de dos rectángulos iguales y divididos en las mismas partes, de las cuales seleccionaremos diez partes iguales.
Otra de las formas utilizadas para representar fracciones es por medio de una recta numérica.
-Fracciones propias
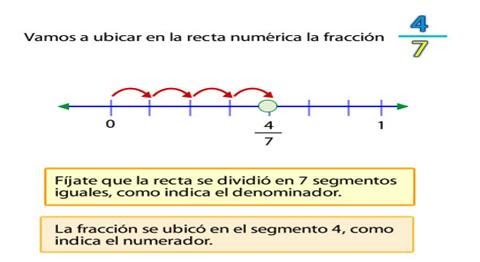
En el caso de las fracciones propias, lo que debemos realizar será dibujar una recta numérica la cual vamos a dividir en tantas partes o segmentos iguales, según establezca el denominador de la fracción. Luego procedemos a ubicar la fracción en la recta numérica según indica el numerador. Por ejemplo: Queremos representar en recta numérica la fracción de 4/7.
Lo primero a realizar será dividir la recta en siete segmentos iguales, tal como indica su denominador. Luego ubicamos la fracción en el segmento cuatro (que es el que indica el numerador).
-Fracciones impropias
En el caso de las fracciones impropias tenemos dos formas de representarlas en una recta numérica:
–Directamente: Esto es por medio de la división de todos los números enteros de la recta numérica en partes o segmentos, dependiendo de la cantidad que indique el denominador. Comenzando desde cero contaremos el número de veces que indica el numerador y ahí ubicamos la fracción.
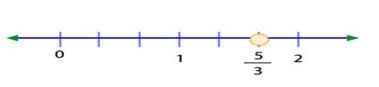
–Transformando la fracción impropia en un número mixto: Para esto debemos dividir el numerador de la fracción por el denominador. Así obtendremos un numero mixto, en donde el numero entero nos indicará entre que números esta la fracción impropia y la fracción resultante se ubicara entre dichos números.
Ejemplo:
Ejercicios para practicar gráficos de fracciones
A continuación te dejamos fracciones para que puedas practicar la representación de las mismas:
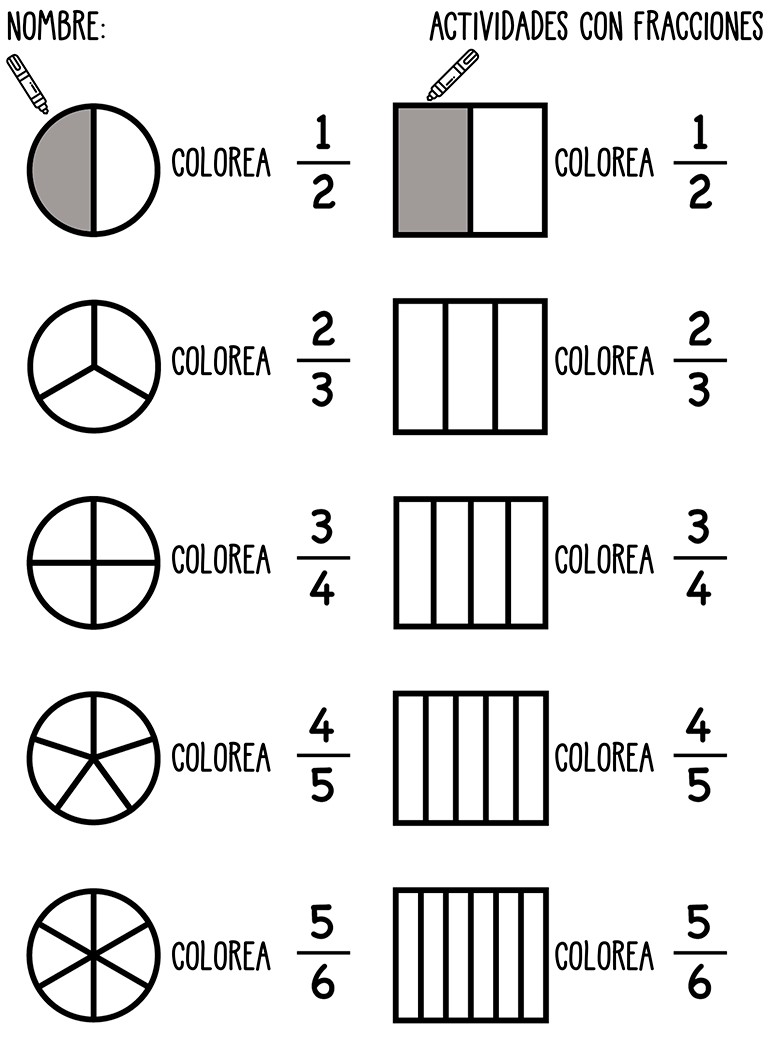
- Representar mediante una figura geométrica las siguientes fracciones: 4/8, 6/10, 8/5
- Representar mediante una recta numérica las siguientes fracciones: 5/7, 3/5, 8/6