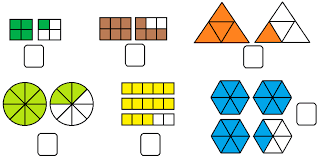Actualizado 6 noviembre, 2020
Las fracciones son la representación de las partes de un todo, esto quiere decir que al dividir algo en partes iguales y seleccionar una cantidad determinada de esta, la forma que tenemos de representarlo será a través de las fracciones.
Existen diferentes tipos de fracciones, en el día de hoy conoceremos al detalle cuales son las fracciones propias y las fracciones impropias.
¿Qué son las fracciones?
Se denomina como fracción al número que se obtiene de dividir un entero en partes iguales. Por ejemplo si tenemos la cuarta parte de una pizza, significa que estamos dividiendo la misma en cuatro partes igual y solo tomamos una porción de ella (1/4).
Las fracciones pueden expresarse como su resultado, es decir, un número único ya sea entero o decimal, es así que todas ellas pueden ser reexpresadas como números. De manera opuesta también todos los números pueden ser reexpresados como fracciones, aquellos números que son enteros se conciben como fracciones con denominador uno. Por medio de las fracciones lo que estamos dividiendo es un número entero y cada parte es una fracción de dicho entero.
Con respecto a la representación grafica de las fracciones, la forma de escribirlas es unos números por encima de los otros y separados por una línea recta horizontal denominada raya fraccionaria. Al número que está arriba de la raya se lo conoce como numerador, al que está abajo como denominador y este último es el que actúa como divisor.
El numerador implica la cantidad de partes que se consideran del total o de la unidad. Por su lado el denominador es el número de partes iguales en que se haya dividido el total o la unidad.
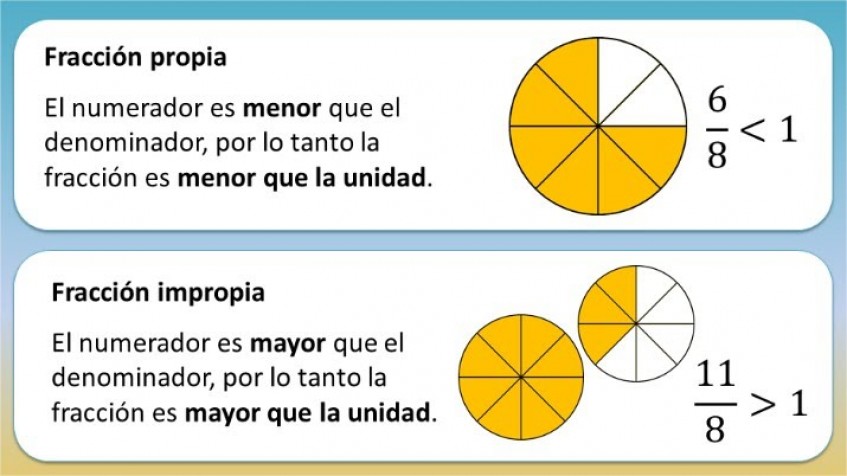
Por ejemplo: si miramos la fracción 5/8 la misma representa 5 dividido 8, esto equivale a 0,625. Si el numerador es mayor que el denominador implica que la fracción es mayor que la unidad, y por tal razón puede ser reexpresada como un valor entero más una fracción menor de 1.
Otro aspecto a tener en cuenta es que el mismo número puede ser reexpresado por una cantidad infinita de fracciones, por ejemplo 5/8 será igual a 10/16, a 15/24 y a 5000/8000, y siempre serán equivalentes a 0,625. Estas fracciones son denominadas equivalentes y siempre mantienen una relación de proporcionalidad directa.
Teniendo en cuenta que las fracciones son relaciones proporcionales entre dos números, se establece una diferenciación entre aquellas que superan la unidad y las que no la superan. Estamos hablando de las fracciones impropias y las fracciones propias.
Fracciones impropias
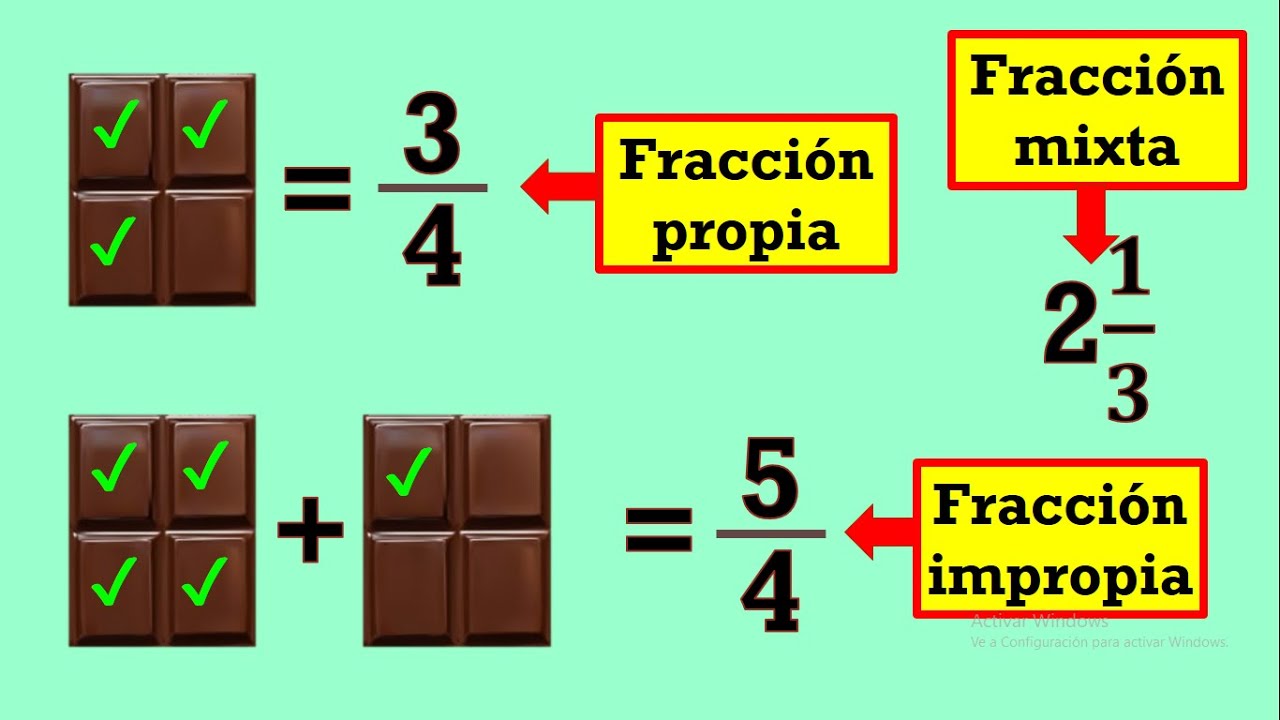
Las fracciones impropias son aquellas en las que el numerador, es decir el numero que se encuentra por encima de la raya fraccionaria, es siempre mayor que el numero del denominador (es decir el que esta por debajo). Esta fracción puede ser también expresada como una combinación entre un número entero y otro fraccionario y menor que uno. Se habla de combinación, ya que en la escritura se puede ver al numero entero y a su derecha al numero fraccionario, si bien formalmente correspondería que se escriba con el signo +, por lo general esto no se hace.
Estos números que están compuestos por un entero y una fracción son llamados números mixtos y es común verlos en los carteles de los comercios que venden mercadería al peso. Por ejemplo: si estamos en una heladería, es muy poco probable que alguien pida 5/2 de kilo de helado, sino que va a pedir dos kilos y medios (2 ½).
Para poder convertir una fracción impropia en un número mixto hay que descomponer el numerador de tal manera que logre ser divisible por el denominador y dando de este modo como resultado un número entero. Por ejemplo: 4/2 = 2.
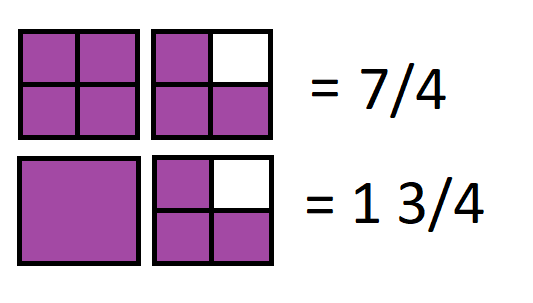
Desde el punto de vista matemático, no sirve expresar una fracción impropia como la cantidad de unidades que tiene y el cociente menor de uno, ya que lo que verdaderamente importa es cada numero por separado. Las operaciones entre fracciones, como así también las que combinan fracciones y números enteros, son mucho más fáciles y sencillas cuando se trabaja con fracciones impropias.
Si bien las operaciones entre fracciones propias e impropias se realizan de la misma forma, si existen determinadas características que diferencian a un caso de otro. Tal es así que por ejemplo una multiplicación entre fracciones impropias nos arroja como resultado una fracción impropia.
La división entre fracciones impropias si depende de que numero se ubica en el numerador y cual numero se ubica en el denominador. Si el numerador es mayor que el denominador, estamos frente a una fracción impropia, a la inversa si el numero que se encuentra en el numerados es menor que el del denominador estamos frente a una fracción propia.
Un caso a tener en cuenta dentro de las fracciones impropias, son aquellas que resultan de una división en la que no hay resto, esto quiere decir que el numerador es múltiplo del denominador entonces estamos frente a un numero entero. Estas fracciones son llamadas aparentes.
Ejemplos de fracciones impropias
Algunos ejemplos de fracciones impropias son:
100/17
21/11
21/9
72/34
5/2
98/50
41/8
Fracciones propias
Las fracciones propias son aquellas fracciones que resultan de la división entre dos números, en los cuales el numerador o también llamado dividendo, es menor que el denominador o también llamado divisor (numero ubicado por debajo de la raya fraccionaria).
Este tipo de fracciones son expresadas por medio de un número menor a uno, es decir un número fraccionario.
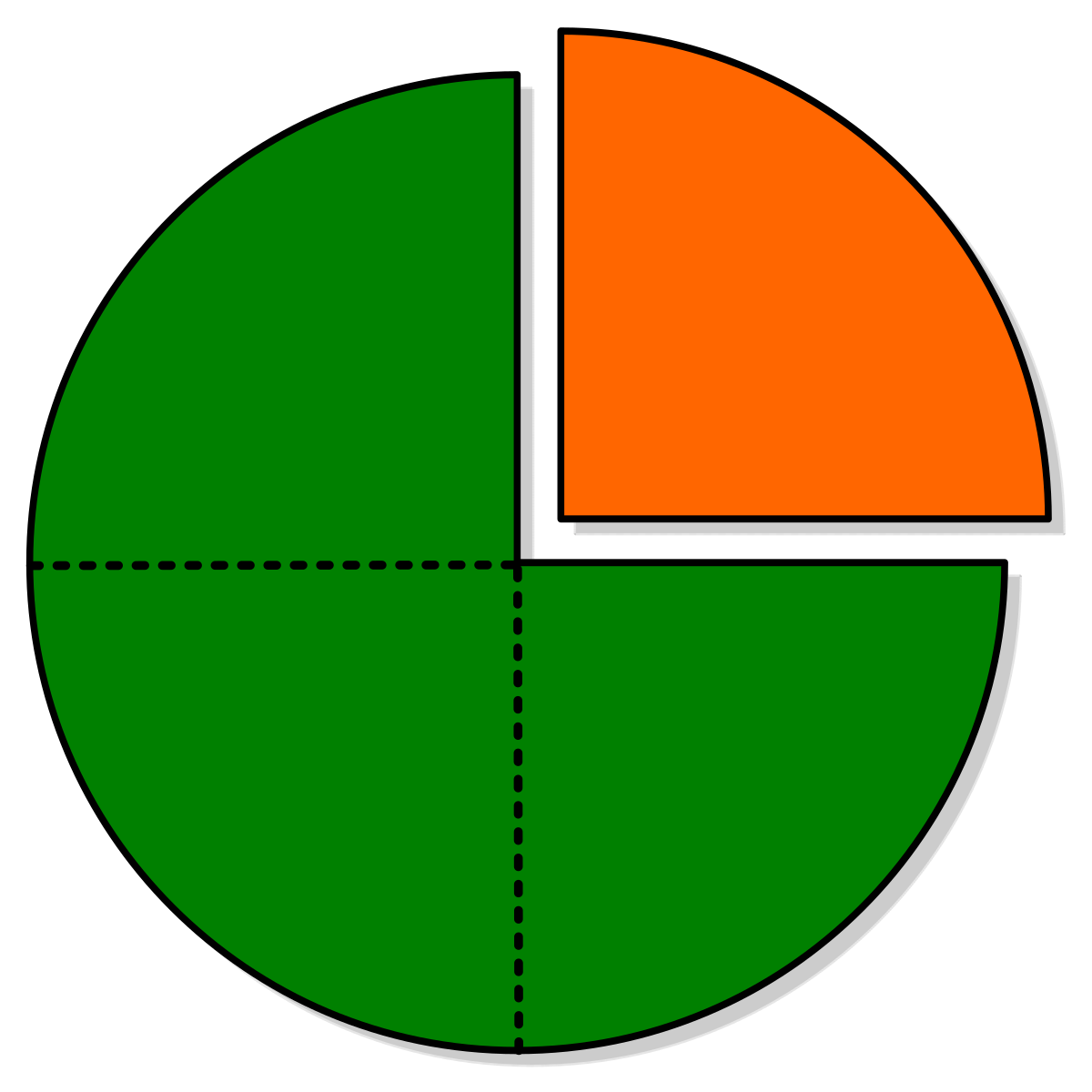
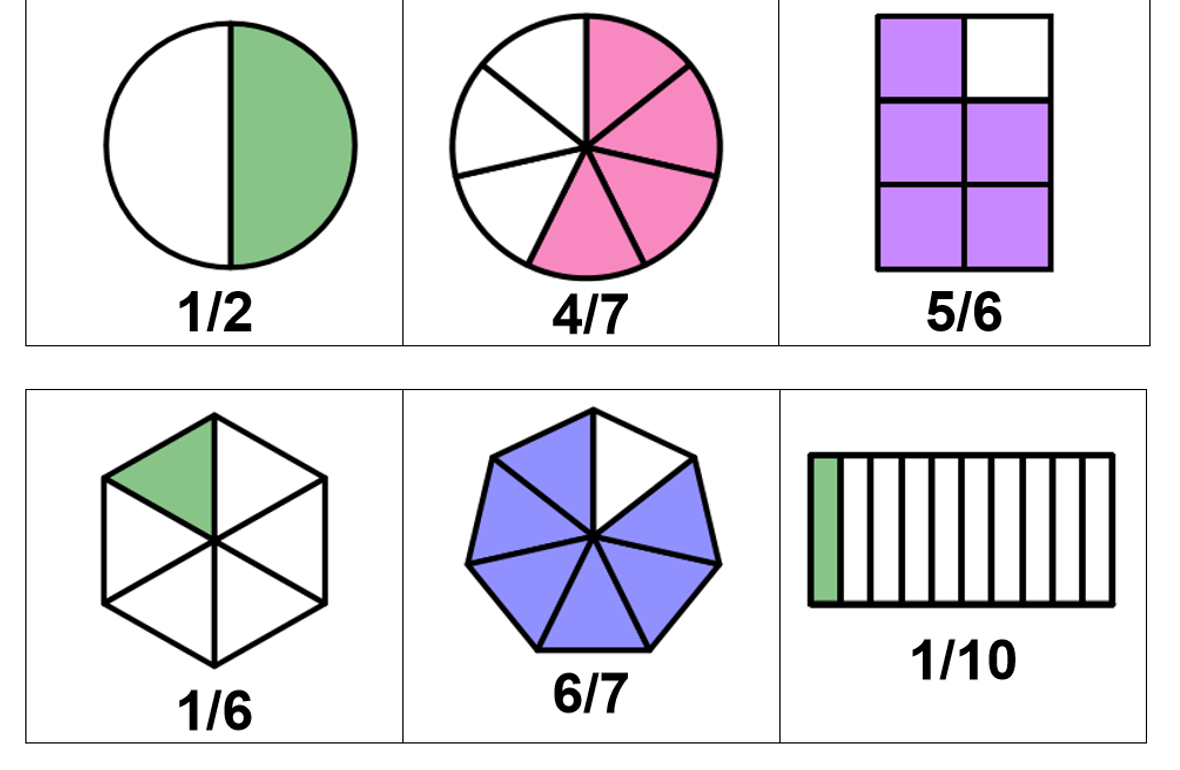
El concepto de este tipo de fracciones es muy sencillo: se necesita graficar una figura geométrica que es fácilmente divisible en partes iguales, por ejemplo un círculo o redondel en el cual se pueden marcar las partes a modo de porciones y dividirlo en tantas partes iguales como el número que tengamos en el denominador. Una vez realizado esto podemos colorear tantas partes como determina el número que tengamos en el numerador y de este modo tendremos representada la fracción propia.
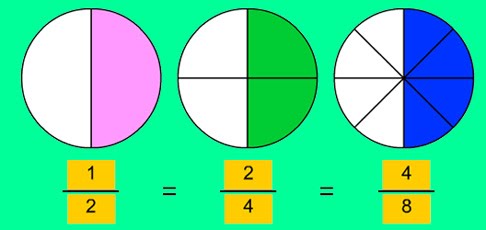
En la cotidianidad es muy común encontrar este tipo de fracciones, por ejemplo en el peso de determinados alimentos (medio kilo, un cuarto de kilo, tres cuartos de kilo, etcétera). Como vemos estas son fracciones propias en donde el numerador es menor que el denominador.
Una de las características principales de este tipo de fracciones es que pueden ser expresadas por medio de porcentajes, ya que suele ser común expresar las proporciones con respecto al numero cien. Para poder hacer esta conversión se debe buscar cual es el numerador que transforme la fracción en una equivalente de denominador cien, a través de la famosa regla de tres.
Por ejemplo: Si A (numerador) es a B (denominador), como es C a 100. Siendo C el número porcentual que queremos encontrar.
Las fracciones propias, a diferencia de las fracciones impropias, no pueden ser reexpresadas como una combinación entre un número entero y un número fraccionario, ya que esto implicaría que el número entero sea cero.
Las operaciones realizadas entre fracciones propias siguen las reglas generales de las operaciones entre fracciones. Estas son: para sumas y restas se necesita buscar un denominador común por medio de las fracciones equivalentes. Por su parte para las operaciones de productos y cocientes no resulta necesario realizar ese procedimiento. El producto entre dos fracciones propias, siempre será una fracción del mismo tipo, en cambio el cociente o división entre dos fracciones propias necesitará que la más grande haga las veces de denominador para lograr ser también una fracción propia.
Ejemplos de fracciones propias
Algunos ejemplos de fracciones propias son:
25/7
2/5
40/90
10/15
65/130
1/100
10/200
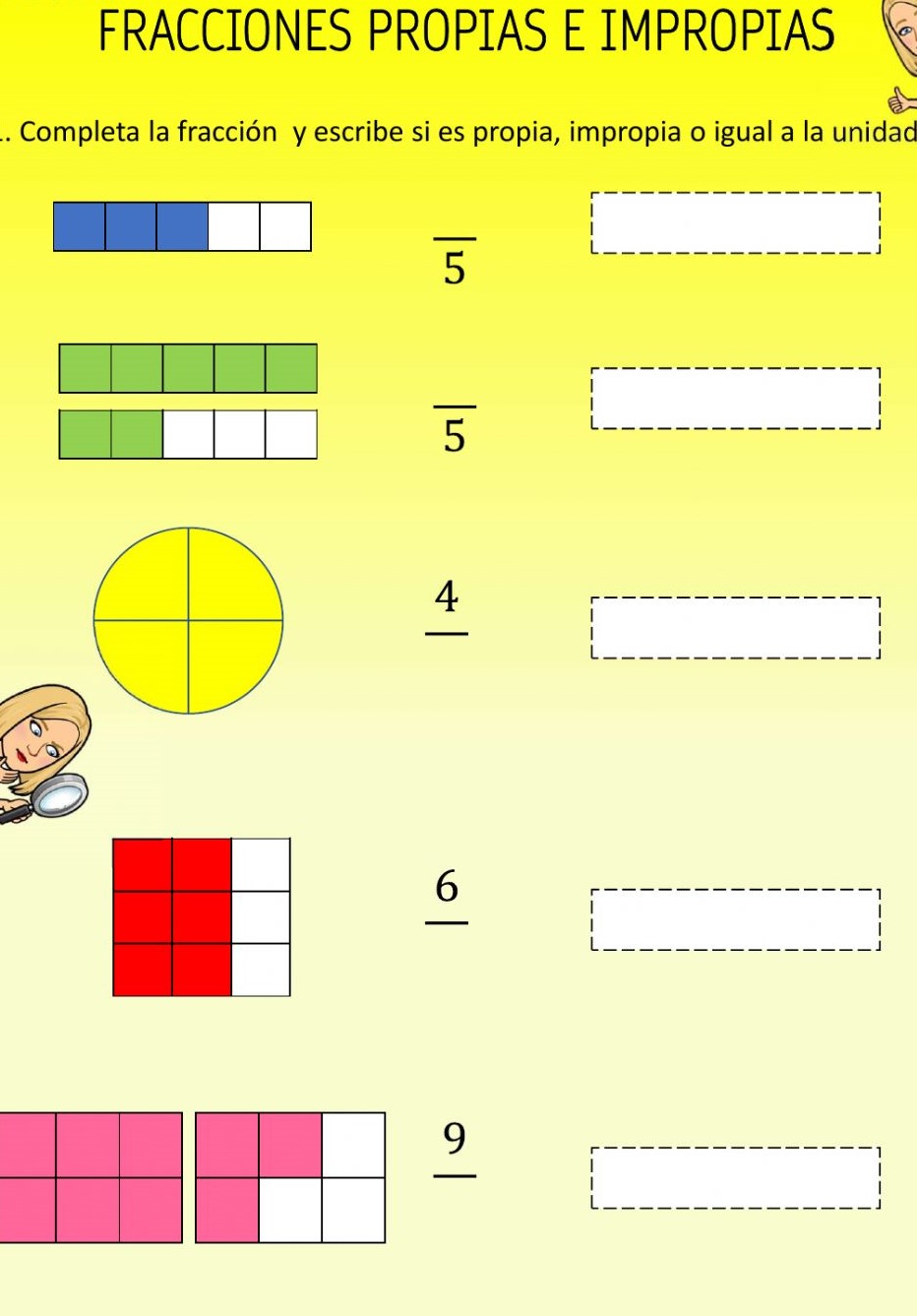
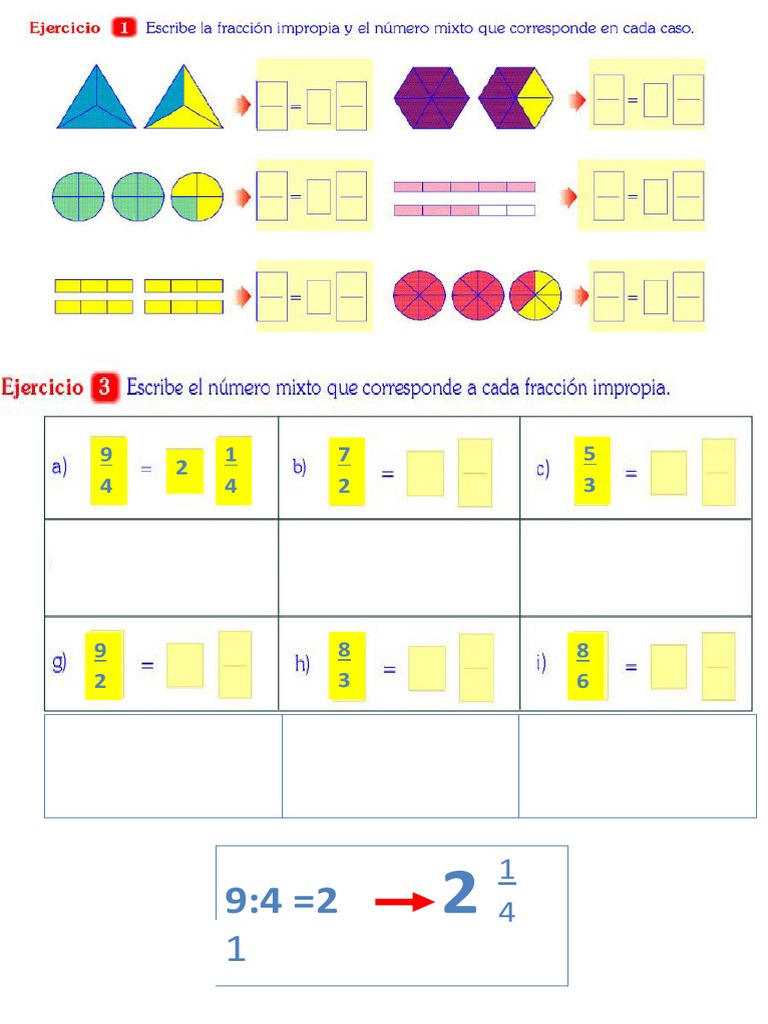
Ejercicios