Actualizado 27 febrero, 2021
Las fracciones representan partes iguales de un todo o una colección. Se dice fracción de un todo cuando dividimos un todo en partes iguales y cada parte es una fracción del todo. En esta oportunidad te queremos regalar información sobre las fracciones para que puedas aprender un poco mas sobre matemáticas y puedas enseñarle a los mas pequeños sobre este tema. También te vamos a mostrar ejercicios que te ayudaran a comprender toda la información que te brindamos aquí. Así que disfruta de todo este contenido y comparte el que quieras.
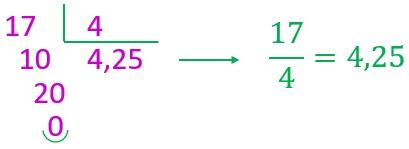
¿Qué son las fracciones?
Una fracción es un número que representa un número entero que se ha dividido en partes iguales. Por ejemplo, si tiene un pastel y lo corta en 4 porciones iguales, 1 de esos porciones se escribe como ¼. Una fracción también puede representar una parte de un grupo. Por ejemplo, si tienes 5 caramelos y le das 2 a tu amigo, esos 2 caramelos se escriben como 2/5. Una fracción esta formada por dos partes. El número en la parte superior de la línea se llama numerador e indica cuántas partes iguales del conjunto o colección se toman. El número que esta por debajo de la línea se llama denominador y muestra el número total divisible de partes iguales del todo o el número total de partes iguales que hay en una colección.
Las fracciones se clasifican en:
Fracciones unitarias
Las fracciones con numerador 1 se denominan fracciones unitarias.
Fracciones propias
Las fracciones en las que el numerador es menor que el denominador se denominan fracciones propias.
Fracciones impropias
Las fracciones en las que el numerador es mayor o igual que el denominador se denominan fracciones impropias.
Fracciones mixtas
Las fracciones mixtas constan de un número entero junto con una fracción propia.
¿Qué son las fracciones equivalentes?
En matemáticas, las fracciones equivalentes se pueden definir como fracciones con diferente numerador y denominador, y que representan el mismo valor o proporción del todo. Las fracciones equivalentes representan la misma distancia o puntos en una recta numérica. Todas las fracciones equivalentes se reducen a la misma fracción en su forma más simple.
Las fracciones equivalentes tienen el mismo valor, aunque pueden verse diferentes.
Estas fracciones son realmente las mismas:
1/2 = 2/4 = 4/8
¿Por qué son iguales? Porque cuando multiplicas o divides tanto la parte superior como la inferior por el mismo número, la fracción mantiene su valor.
La regla para recordar es:
Cambiar la parte inferior usando multiplicar o dividir, Y se debe aplicar lo mismo en la parte superior.
Ejercicios con fracciones
Con las fracciones se puede hacer operaciones matemáticas como la suma, resta, multiplicación y división. A continuación te vamos a explicar como hacerlas.
Suma: cuando las fracciones tienen el mismo denominador se realiza la suma de los numeradores y se coloca el mismo denominador en el resultado.
1/4 + 6/4 = 7/4
Cuando el denominador no es el mismo se debe buscar un denominador común para poder realizar la suma. Para buscar un denominador común se deben buscar fracciones equivalentes de forma que ambas tengan el mismo denominador.
Resta: cuando las fracciones tienen el mismo denominador deben restarse los numeradores y se coloca el mismo denominador en el resultado.
4/5 – 2/5 = 2/5
Cuando el denominador no es el mismo se debe buscar un denominador común para poder realizar la resta. Para buscar un denominador común se deben buscar fracciones equivalentes de forma que ambas tengan el mismo denominador.
Multiplicación: esta operación es muy fácil de hacer. Se debe multiplicar los numeradores y luego los denominadores para obtener el resultado. No hace falta buscar denominador común.
2/5 x 3/4 = 6/20
División: para hacer esta operación debes multiplicar las fracciones en cruz. Se debe multiplicar el numerador de la primera fracción por el denominador de la segunda fracción, y el denominador de la primera fracción por el numerador de la segunda fracción.
2/3 % 5/4 = 2 x 4 / 3 x 5 = 8/15
¿Que son los números decimales?
Los números decimales se utilizan para representar números menores a 1 unidad. Los decimales se escriben a la derecha del lugar de las unidades separados por un punto. Los números decimales se pueden definir como un número cuya parte numérica y la parte fraccionaria están separadas por un punto decimal. El punto en un número decimal se llama punto decimal. Los dígitos que siguen al punto decimal muestran un valor menor que uno. Aquí hay un ejemplo de un número decimal 17.48, en el que 17 es el número entero, mientras que 48 es la parte decimal. Los decimales se basan en la potencia anterior de 10. Por lo tanto, a medida que nos movemos de izquierda a derecha, el valor posicional de los dígitos se divide por 10, lo que significa que el valor posicional decimal determina las décimas, centésimas y milésimas. Un décimo significa un décimo o 1/10. En forma decimal, es 0,1. Centésimo significa 1/100. En forma decimal, es 0.01.
las fracciones y los números decimales se relacionan:
Las décimas son 1 unidad dividida en 10 partes iguales = 1/10 = 0,1.
Centésimas son 1 unidad dividida en 100 partes iguales = 1/100 = 0.01.
Milésimas son 1 unidad dividida en 1,000 partes iguales = 1 / 1,000 = 0.001.
¿Cuales son los Tipos de números decimales?
Los números decimales se pueden clasificar según si tiene un número limitado o infinito de cifras decimales. Los números decimales pueden ser:
Decimales exactos: son aquellos que tienen un número limitado de cifras decimales. Por ejemplo: 1,745
Decimales no exactos: son aquellos que en su parte decimal tienen un número infinito de cifras decimales. Los números decimales no exactos pueden ser periódicos o no periódicos.
Decimales periódicos: son decimales periódicos si en la parte decimal existe una cifra o un grupo de cifras que se repiten indefinidamente. Este grupo de cifras se llama período. El período se simboliza con un arco encima del conjunto de números que se repiten. Ejemplo: 3,161616
Decimales no periódicos: tiene un número infinito de cifras decimales (ilitimadas cifras), y en estas cifras no existe ninguna cifra o grupo de cifras que se repitan de manera indefinida. Ejemplo: 3,141592
Los decimales periódicos pueden ser:
Decimales periódicos puros: son periódicos decimales puros cuando toda su parte decimal es periódica. Es decir, las cifras que componen el período comienzan inmediatamente después de la coma. Ejemplo: 3,131313
Decimales periódicos mixtos: cuando tiene cifras decimales antes del período que no se repiten. A estas decimales se les llama cifras anteperíodo. Ejemplo: 12,253333
Como convertir fracciones a números decimales
A cada fracción le corresponde un número decimal. Para convertir una fracción en números decimales tenemos dividir el numerador entre el denominador como haríamos una división de dos números normales. Según el tipo de numero decimal que da la fracción existen tres tipos de casos:
Fracción decimal exacta
La fracción decimal exacta es la que, al dividir el numerador y el denominador, se llega a obtener un resto igual a cero y un número de decimales limitado en el cociente.
Ejemplo: 14/8
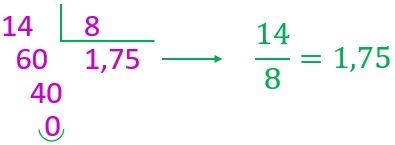
Fracción periodica pura
La fracción periódica pura es aquella que al hacer la división de los dos términos de la fracción, nunca se llega a obtener un residuo cero, y se va repitiendo las cifras del cociente periódicamente, a partir de la coma.
Ejemplo: 11/3
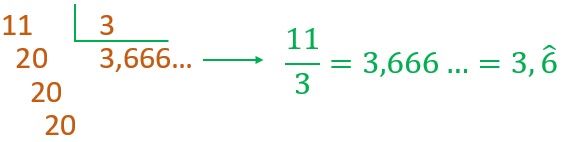
Fracción periodica mixta
La fracción periódica mixta es aquella que al hacer la división de los dos términos de la fracción, nunca se llega a obtener un residuo cero, y se repiten las cifras del cociente periódicamente, pero no justamente después de la coma.
Ejemplo: 77/15
Ejercicios para convertir fracciones en números decimales
A continuación te vamos a mostrar ejercicios para que aprendas a convertir fracciones en números decimales sin problemas. Así que sigue disfrutando de este blog y aprende un poco mas sobre las matemáticas.
Expresar en forma decimal:
1/2 =
(0,5)
3/4 =
(0,75)
2/3 =
(0,6666)
9/5 =
(1,8)
8/1 =
(8)
8/5 =
(1,6)
5/8 =
(0,625)
6/18 =
(0,3333)
60/4 =
(15)
Espero que te haya gustado toda la información sobre los decimales y las fracciones que te regalamos aquí…