Actualizado 23 julio, 2020
Las fracciones son conocidas también como números racionales o quebrados, y las mismas representan la parte de un todo. Es decir, por medio de las fracciones lo que estamos dividiendo es un entero y cada parte es una fracción de dicho entero.
Con las fracciones podemos hacer las operaciones matemáticas de suma, resta, división y multiplicación. A continuación explicaremos como realizar las restas de fracciones, veremos ejemplos y ejercicios.
¿Qué son las fracciones?
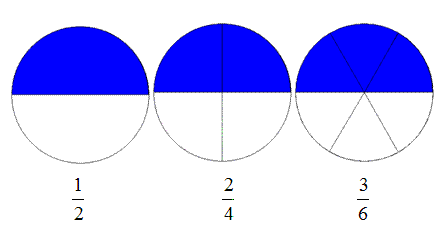
Tal como decíamos las fracciones son la representación de las partes de un todo. Este concepto quiere decir que al dividir algo en partes iguales y tomar una determinada cantidad de esta, la forma que tenemos de representarlo es por medio de las fracciones.
Los números que componen una fracción se representan separados por una recta horizontal. En la parte superior encontraremos al llamado numerador y en la parte inferior se encuentra el denominador.
El numerador expresa a las partes que se han tomando de un todo y el denominador indica el total de partes en que se dividió el entero (que es el numerador).
Veamos un ejemplo para entenderlo bien:
Suponiendo que tenemos una hoja de papel y la dividimos en partes iguales, cada una de estas partes representara a una porción del todo. Si dividimos el papel en cuatro, cada una de estas partes representará un cuarto (1/4) del todo (que es cuatro cuartos 4/4).
En este caso el número cuatro representa al denominador y siempre será el mismo.
Tipos de fracciones
Podemos encontrar distintos tipos de fracciones. Veamos al detalle cada una de ellas:
- Fracción propia
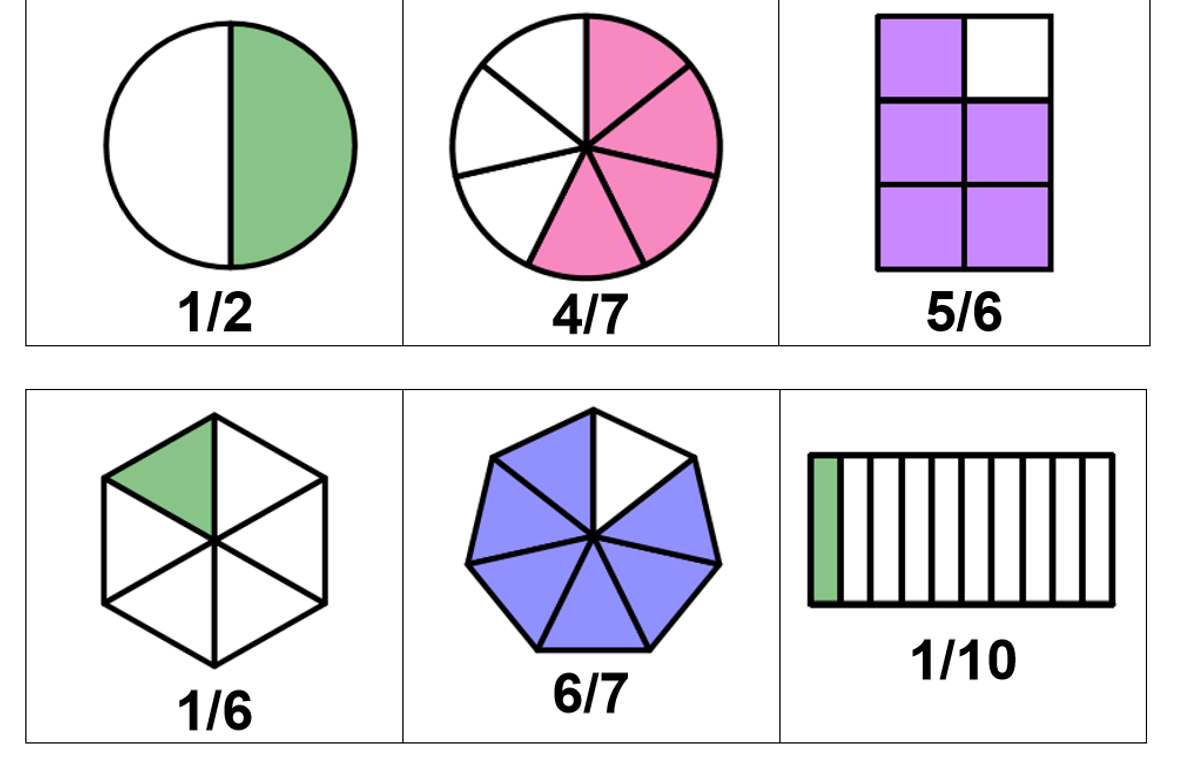
Se conoce como fracción propia a aquella en la cual el numerador es menor que el denominador, esto implica que la fracción representa un numero mas chico que un entero. Algunos ejemplos: un cuarto (1/4), dos octavos (2/8), dos cuartos (2/4).
- Fracción impropia
Las fracciones impropia son aquellas en las cuales el numerador es mayor que el denominador, esto implica que estas fracciones representan un número mas grande que el entero. Por ejemplo: diez tercios (10/3), cuatro medios (4/2), ocho medios (8/2).
- Fracciones comunes y decimales
Se denominan fracciones comunes a aquellas cuyo denominador no es la unidad seguida de ceros. Por ejemplo: dos sextos (2/6), un octavos (1/8), nueve onceavos (9/11). Y se denomina como fracciones decimales, a aquellas fracciones cuyo denominador si es la unidad seguida de ceros. Por ejemplo: tres decimos (3/10), una centésima (1/100), diez milésimas (10/1000).
- Fracciones mixtas
Son aquellas fracciones que están compuestas por un numero entero y una fracción propia, que se escriben juntos o combinados. Por ejemplo: 3 3/2.
- Fracciones homogéneas
Se denomina fracciones homogéneas a aquellas que poseen igual denominador. Si dos fracciones tienen el mismo denominador positivo la fracción mayor será la que mayor numerador tiene.
- Fracciones equivalentes
Se conoce como fracciones equivalentes a aquellas fracciones que son iguales.
Resta de fracciones
Para poder realizar resta de fracciones, lo primero que debemos analizar es si las fracciones poseen igual o distinto denominador, ya que en el caso de que tengan diferente denominador deberemos primero igualarlos para luego poder realizar la operación de resta de las fracciones. A continuación explicaremos ambos casos:
Resta de fracciones con igual denominador
Para restar fracciones que poseen igual denominador la forma de proceder será: se restan los numeradores y se mantiene el mismo denominador.
Por ejemplo:
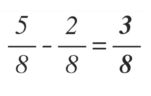
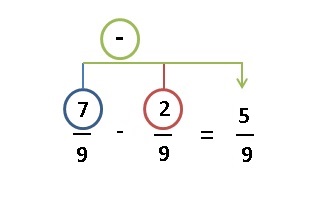
Tenemos la resta de dos fracciones que poseen como denominador común al numero ocho. En este caso restaremos los numeradores y permanece igual el denominador: 5 – 2, es igual a 3 y como denominador dejamos al ocho. De esta manera el resultado de nuestra resta será tres octavos (3/8).
Resta de fracciones con distinto denominador
Cuando se nos presenten casos de restas de fracciones que tienen diferente denominador, lo primero que debemos hacer es buscar un denominador común. Para esto, tenemos que calcular el mínimo común múltiplo de los denominadores. Una vez que tenemos el mcm (mínimo común múltiplo) debemos asignar este resultado obtenido a todos los nuevos denominadores de las fracciones que estamos restando.
Por ultimo debemos dividir el nuevo denominador entre el numerador de cada fracción para poder obtener los nuevos numeradores, y ahora si hacemos la resta de la misma forma que cuando es un caso de igual denominador. En caso de que podamos debemos simplificar el resultado de la operación.
Veamos un ejemplo para entenderlo mejor: Supongamos que tenemos que realizar la siguiente resta
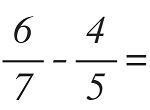
Como vemos estamos ante un caso de fracciones con denominador diferente, por lo tanto lo primero que debemos realizar será buscar el mínimo común múltiplo entre ambos. En el caso presentado en el ejemplo el mcm será el numero 35.
Una vez que tenemos el mínimo común múltiple debemos convertir las fracciones, para esto vamos a poner en el denominador de ambas el numero 35 y vamos a multiplicar cada uno de los denominadores para convertirlos:
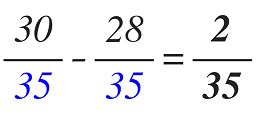
Como vemos, multiplicamos seis por cinco (6 x 5 = 30) y multiplicamos cuatro por siete (4 x 7 = 28). En el denominador de ambas fracciones dejamos el mínimo común múltiple que es 35. Una vez que convertimos las fracciones, realizamos la tradicional resta de los numeradores, en el caso de nuestro ejemplo seria 30 – 28, dando como resultado el numero dos. En el denominador dejamos el mcm (35).
En nuestro ejemplo no es posible simplificar aun más el resultado, pero en caso de que se pueda se debe hacer.
Veamos otro ejemplo:
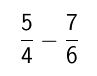
Como vemos estamos frente a un caso de denominadores diferentes, por lo tanto procedemos a convertir las fracciones en dos de igual denominador. Buscamos el mínimo común múltiple entre cuatro y seis, que es doce (12).
De este modo las dos fracciones tendrán como denominador al doce. Para encontrar el nuevo denominador de ambas fracciones debemos dividir el nuevo denominador (que es el mcm que habíamos encontrado anteriormente) entre el antiguo de denominador y dicho resultado lo multiplicaremos con el antiguo numerador.
En el caso de la primera fracción sería:
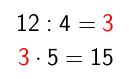
En el caso de la segunda fracción sería:
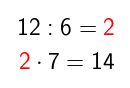
Ahora si, una vez que quedaron convertidas las fracciones con igual denominador, realizaremos la resta como se hace de manera habitual: 15 – 14 = 1.
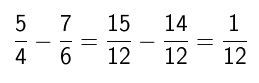
Como podemos ver el resultado de nuestra operación es un doceavo (1/12).
Mínimo común múltiplo
Se conoce como mínimo común múltiplo al número positivo más pequeño que es múltiplo de dos o más números.
-¿Qué son los múltiplos? Los números de un múltiplo son aquellos que se obtienen cuando lo multiplicas por otros números.
-¿Qué es el múltiplo común? Se denomina así al número que es múltiplo a la vez de dos o más números, esto quiere decir que es un múltiplo común a esos números.
-¿Qué es el minino común múltiplo? Llamamos m.c.m al menor o numero más pequeño de esos múltiplos comunes.
¿Cómo calculamos el minino común múltiplo?
Para poder encontrar ese múltiplo común de dos o más números lo primero que debemos hacer es:
1)Buscar los primeros múltiplos de cada número.
2)Seleccionamos los múltiplos que sean comunes entre ambos números.
3)Elegimos el múltiplo común más pequeño.
Otro método posible para calcular el minino común múltiplo es:
1)Lo primero a realizar será descomponer en factores primos cada uno de los números.
2)Seleccionar los factores comunes entre los números que estamos analizando, pero no los comunes elevados al mayor exponente.
3)Por últimos debemos multiplicar los factores elegidos.
Ejercicios para practicar la resta de fracciones:
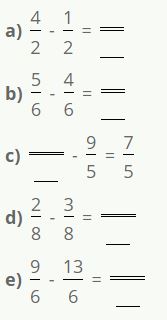
Esperamos que hayan podido entender como realizar la resta de fracciones y pongan en practica los ejercicios!