Actualizado 5 octubre, 2020
Una fracción es un número que representa un número entero que se ha dividido en partes iguales. Una fracción se compone de dos partes, el denominador y el numerador. El denominador es el número inferior de la fracción. Es el número que representa la cantidad total. El numerador es el número superior de la fracción. Es el número que representa la parte del todo. Hoy en este blog te queremos regalamos información, imágenes y ejercicios con fracciones para que puedas aprender a reconocerlas y puedas aprender un poco mas sobre las operaciones básicas con fracciones. Así que es una buena idea que sigas disfrutando de este blog tan útil y de toda la información sobre fracciones que te regalamos aquí.
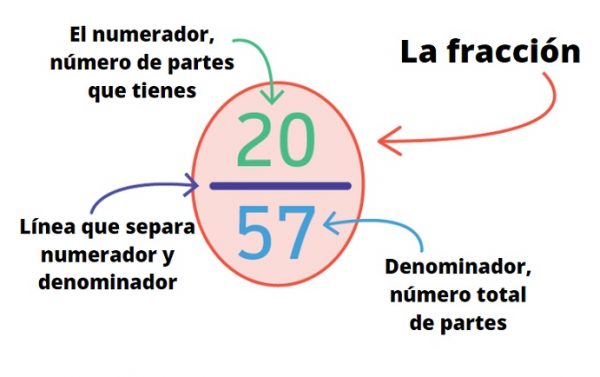
¿Qué son las fracciones?
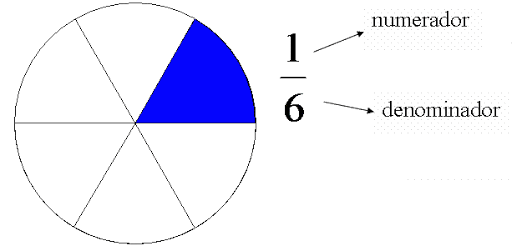
Una fracción, o número fraccionario, se usa para representar una parte de un todo. Las fracciones constan de dos números, por un lado esta el numerador que está arriba de la línea y por otro esta el denominador que está debajo de la línea. El denominador te dice el número de partes iguales en las que se divide algo. El numerador te dice cuántas de estas partes iguales se están considerando. Por lo tanto, si la fracción es la ecuación de un pastel, el denominador 5 le dice que el pastel se ha dividido en 5 partes iguales, de las cuales 3 (numerador) están en la fracción. A veces, es útil pensar que la línea divisoria (el medio de una fracción) significa «fuera de». En otras palabras, la ecuación también significa 3 de 5 partes iguales de todo el pastel.
Suma con fracciones
Para sumar fracciones es importante tener un denominador común. Las fracciones que tienen denominadores comunes se denominan fracciones semejantes y las fracciones que tienen distintos denominadores se denominan fracciones distintas. Para sumar fracciones iguales, simplemente suma los numeradores y mantén el mismo (o igual) denominador.
Para sumar fracciones diferentes, primero debes cambiar todos los denominadores a su mínimo común denominador (MCD), también llamado mínimo común múltiplo del denominador. El mínimo común múltiplo del denominador es el número más bajo que se puede dividir uniformemente por todos los denominadores del problema. Es posible que sea necesario cambiar los numeradores para asegurarse de que las fracciones sigan siendo equivalentes a los originales. Cuando tienes todos los denominadores iguales, puedes sumar los numeradores y mantener el mismo denominador.
Por ejemplo,
2/3 + 4/5
Lo primero que debe hacer es encontrar un denominador común entre 3 y 5. Para hacer esto, calculamos el mínimo común múltiplo entre ambos números.
MCM (3,5) = 15
Entonces 15 es el denominador común de las dos fracciones.
Ahora tenemos que multiplicar cada numerador por el número por el que hemos multiplicado el denominador. Para hacer esto, dividimos el MCM por el denominador inicial y multiplicamos el resultado por el numerador de esa fracción.
Para la primera fracción:
15/3 = 5
5 x 2 = 10
Entonces 10 es el numerador de la primera fracción.
Para la segunda fracción:
15/5 = 3
3 x 4 = 12
Entonces 12 es el numerador de la segunda fracción.
Ahora, todo lo que nos queda por hacer es sumar los numeradores:
10 + 12 = 22
Y el resultado de la suma de fracciones es:
10/15 + 12/15 = 22/15
Resta con fracciones
La resta de fracciones se realiza de manera diferente a los números habituales. Normalmente, al restar fracciones te encontrarás con dos tipos de problemas resta de fracciones con igual denominador y resta de fracciones con distinto denominador.
Fracciones que se restan tienen el mismo denominador, por ejemplo:
3/7 – 1/7
Fracciones que se restan tienen diferentes denominadores, por ejemplo:
4/5 – 1/2
Como sabes, las fracciones representan partes del todo. Entonces, cuando estas partes son del todo dividido en el mismo número de partes, es fácil restarlas. Para los problemas con igual denominador, solo necesitamos restar las partes superiores (numerador) de las fracciones y dejar el denominador como tal. Entonces, para resolver el problema en el ejemplo anterior, la solución será:
3/7 – 1/7 = 2/7
Para problemas donde el denominador es diferente, no podemos restar estas fracciones simplemente restando los numeradores. Para resolver estos problemas primero necesitaremos dividirlos en fracciones con el mismo denominador. Para resolver este problema, primero tendremos que observar los denominadores 5 y 2 y ver qué múltiplos de estos números son comunes.
Los múltiplos de 5 son:
5 10 15 20 25
Los múltiplos de 2 son:
2 4 6 8 10 12 14
entonces, en múltiplos de 5 y 2, el mínimo común múltiplo es 10.
ahora, cambiaremos 4/5 y 1/2 en sus fracciones equivalentes con denominador 10.
4/5 – 1/ 2 = 4×2/5×2 – 1×5/2×5
= 8/10 – 5/10
= 3/10
Multiplicación con fracciones
La multiplicación de fracciones es una de las operaciones básicas que permite obtener una tercera fracción que será el producto de las anteriores, al cual se le conoce como Producto o Resultado de la Multiplicación. Para multiplicar fracciones únicamente se tiene un procedimiento ya sea para multiplicación de fracciones con diferente denominador o con el mismo denominador. En la multiplicación de fracciones se multiplican los numeradores de las fracciones y aparte los denominadores. Si es necesario, simplifique o reduzca la fracción. Una fracción se puede simplificar si el numerador (número superior) y el denominador (número inferior) se pueden dividir por el mismo número.
Por ejemplo:
2/5 x 3/2 = 6/10
División con fracciones
La división eso otra de las operaciones básicas con fracciones. Dividir fracciones es muy sencillo. Para dividir dos o más fracciones, se debe multiplicar en cruz. Esto significa multiplicar el numerador (número de arriba) de la primera fracción por el denominador (número de abajo) de la segunda fracción, y así conseguimos el numerador. Para obtener el denominador, tenemos que multiplicar el denominador (número de abajo) de la primera fracción por el numerador (número de arriba) de la segunda fracción.
Ejemplo:
3/4 : 6/10 = 3×10/4×6
= 30/24
El último paso es simplificar la fracción. Como los dos números son múltiplos de 6 podemos dividir el numerador y el denominador entre 6.
30/24 = 5/4
Simplificación de fracciones
Una fracción está en su forma más simple cuando la parte superior e inferior no pueden ser más pequeñas, sin dejar de ser números enteros.
Ejemplo: 2/4 se puede simplificar a 1/2
Para simplificar una fracción se debe dividir la parte superior e inferior por el mayor número que dividirá ambos números exactamente (deben permanecer enteros).
Ejercicios con fracciones para niños
En esta oportunidad te queremos regalar información sobre la suma, resta, multiplicación y división con fracciones, para que puedas aprender estas operaciones básicas de una manera sencilla. Así que sigue disfrutando de este blog.
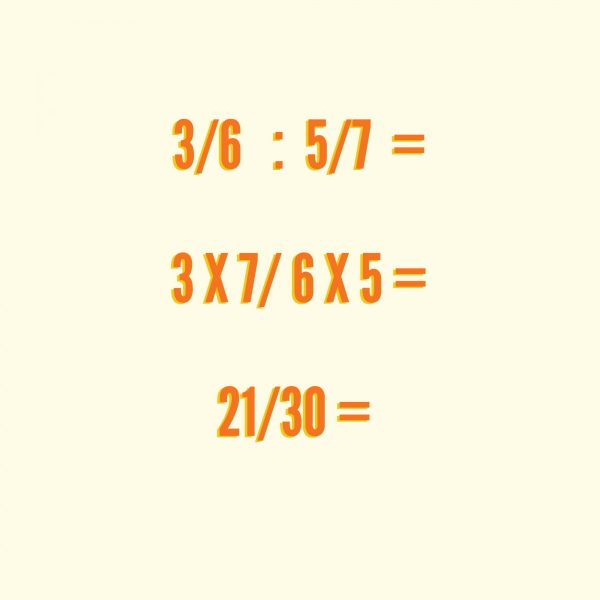
Ejercicio de división con fracciones: se debe multiplicar en cruz. Esto significa multiplicar el numerador de la primera fracción por el denominador de la segunda fracción, y así conseguimos el numerador. Para obtener el denominador, tenemos que multiplicar el denominador de la primera fracción por el numerador de la segunda fracción.
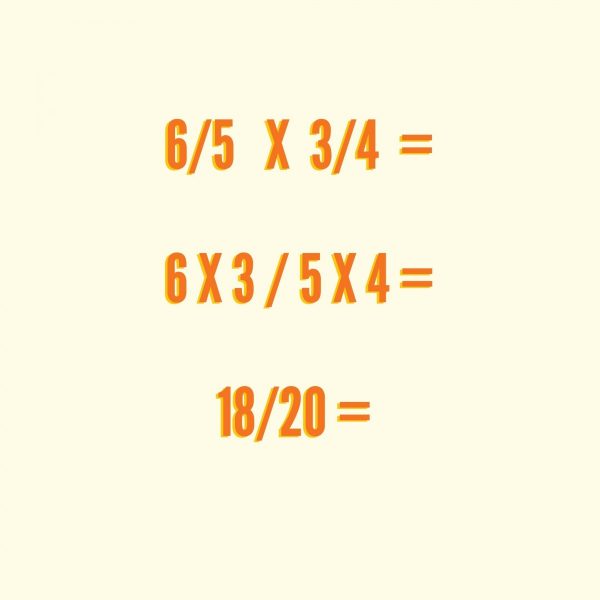
Ejercicio de multiplicación con fracciones para practicar fracciones.
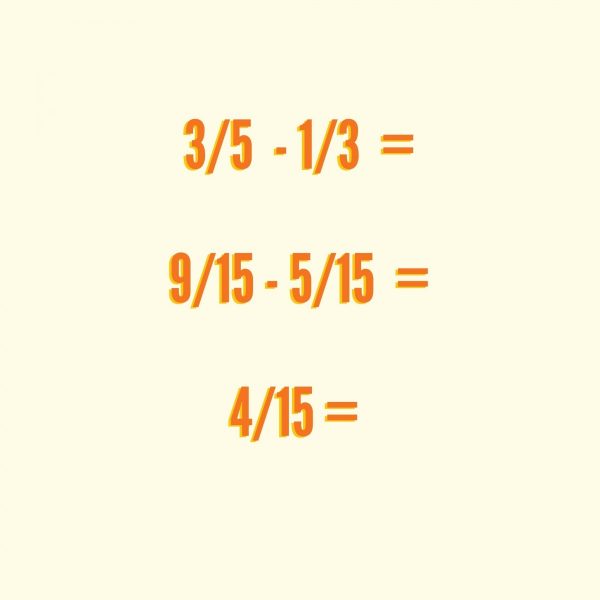
Ejercicio con resta de fracciones con mismo denominador.
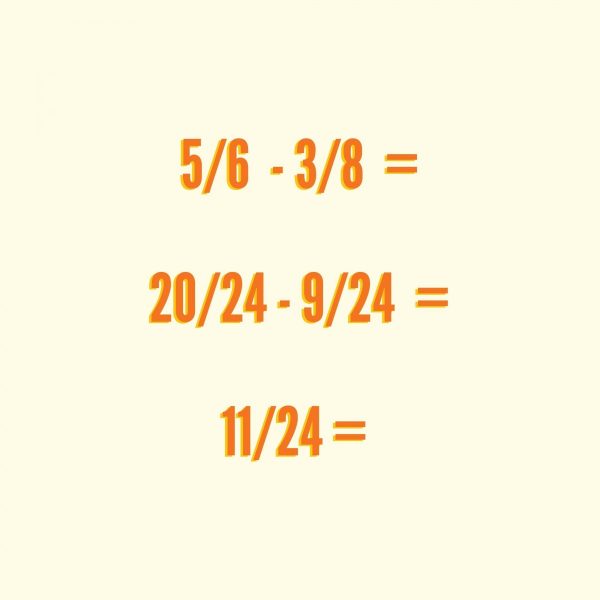
Ejercicio de resta con fracciones de distinto denominador para que puedas practicar una de las operaciones básicas de las fracciones.
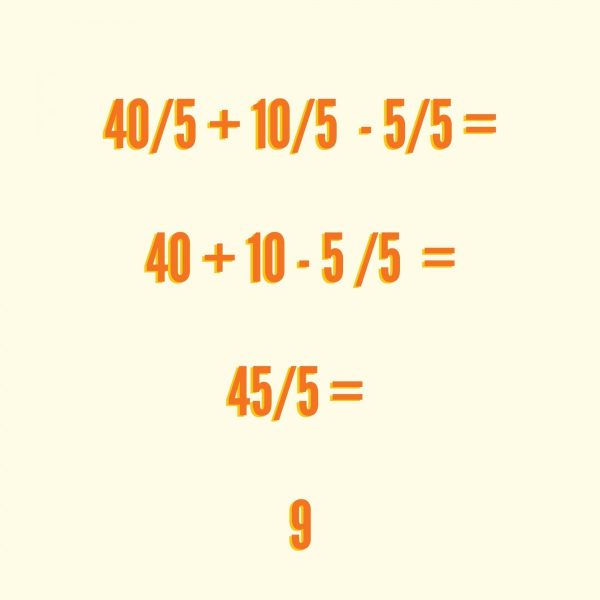
Ejercicio de suma y resta con fracciones de igual denominador que te serviran para agilizar tu mente y aprender a hacer ejercicios con fracciones simples.
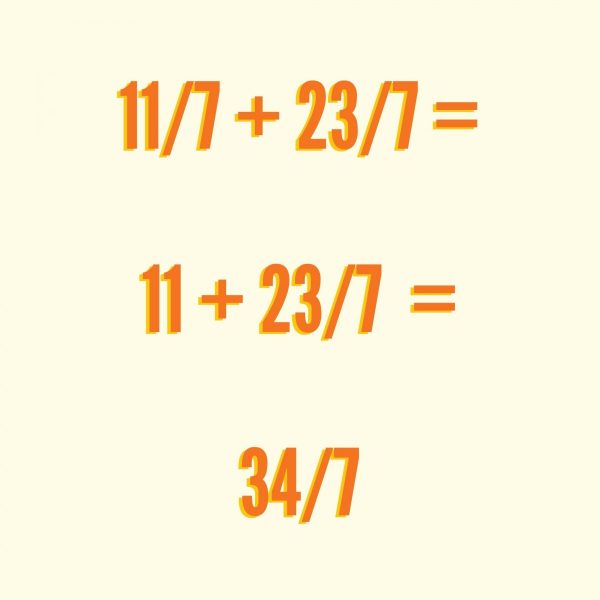
Suma con fracciones con el mismo denominador para ejercitar.
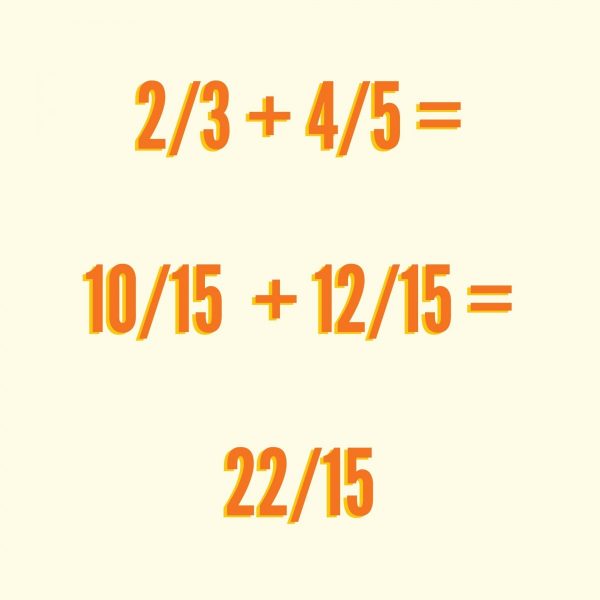
Ejercicio con suma de fracciones con distinto denominador para descargar y practicar las operaciones básicas de las fracciones.
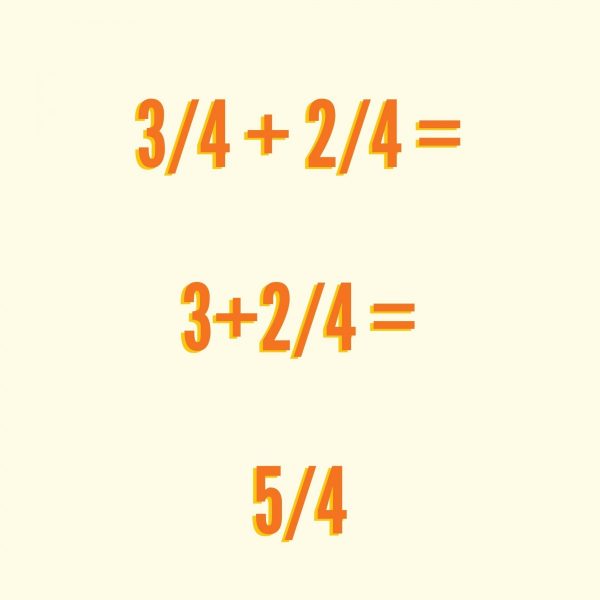
Ejercicio con suma de fracciones con el mismo denominador.
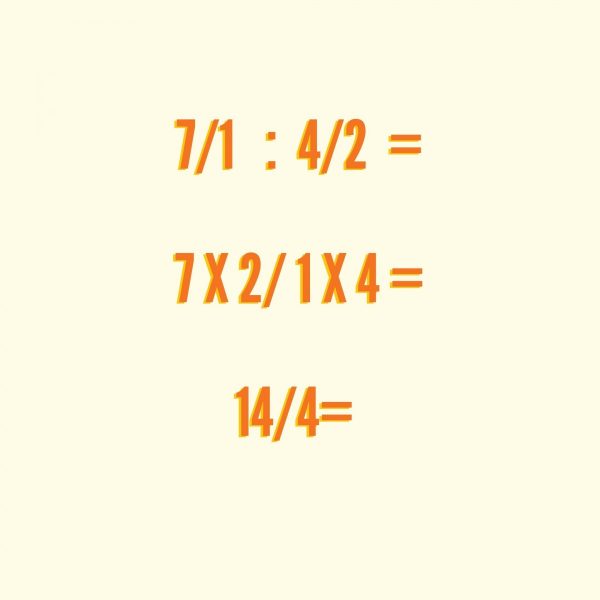
Ejercicio con una división de fracciones que tienen distinto denominador para ejercitar y aprender a hacer estas operaciones de una manera rápida.
Espero que te haya gustado toda la información que te regalamos aquí sobre fracciones y sus operaciones básicas…