Actualizado 19 octubre, 2021
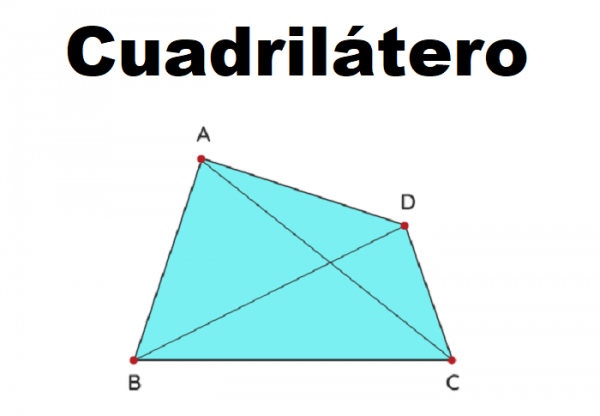
En geometría, un cuadrilátero es una forma cerrada que se forma al unir cuatro puntos entre los cuales tres puntos no son colineales. El mismo tiene 4 lados, 4 ángulos y 4 vértices. Cuadrilátero se deriva de una palabra latina, en la que «Quadra» significa cuatro y «Latus» significa lados. Los 4 lados de un cuadrilátero pueden ser iguales o no.
Definición de cuadrilátero
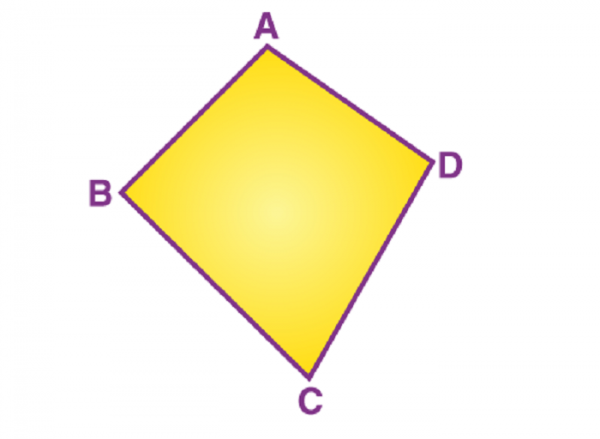
Un cuadrilátero es un polígono con cuatro lados, cuatro ángulos y cuatro vértices. Siempre que nombramos un cuadrilátero, debemos tener en cuenta el orden de los vértices. Por ejemplo, el siguiente cuadrilátero debe denominarse ABCD, BCDA, ADCB o DCBA. No se puede nombrar como ACBD o DBAC, ya que cambian el orden de los vértices en los que se forma un cuadrilátero. A su vez, ABCD tiene cuatro lados: AB, BC, CD, DA y dos diagonales: AC y BD.
Tipos de cuadriláteros
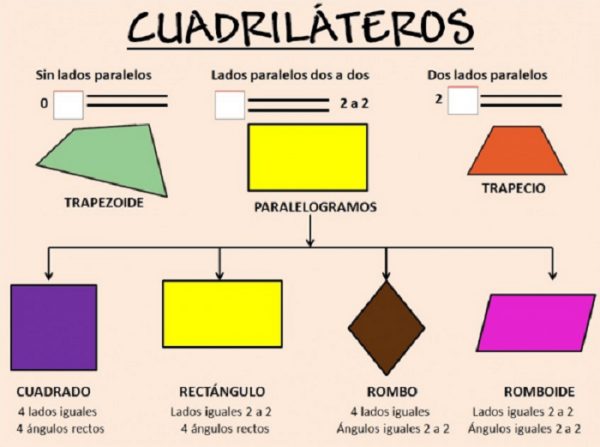
Aunque un cuadrilátero siempre tiene cuatro lados, cuatro ángulos y cuatro vértices, la medida de los lados y los ángulos difiere. Cabe señalar que la suma de los ángulos interiores de un cuadrilátero es siempre igual a 360°. La siguiente tabla enumera los diferentes tipos de cuadriláteros.
La lista de tipos de cuadriláteros son:
- Trapecio
- Paralelogramo
- Cuadrado
- Rectángulo
- Rombo
- Cometa
Cuadriláteros convexos, cóncavos e intersectantes
Otra forma de clasificar los tipos de cuadriláteros son:
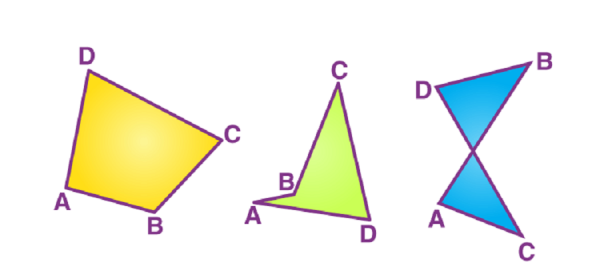
- Cuadriláteros convexos: ambas diagonales de un cuadrilátero están completamente contenidas dentro de una figura.
- Cuadriláteros cóncavos: al menos una de las diagonales se encuentra parcial o totalmente fuera de la figura.
- Cuadriláteros intersectantes: Los cuadriláteros que se cruzan no son cuadriláteros simples en los que el par de lados no adyacentes se cruzan. Este tipo de cuadriláteros se conocen como cuadriláteros auto-intersectantes o cruzados.
Propiedades de los cuadriláteros
Cada uno de los cuadriláteros discutidos anteriormente tiene sus propias propiedades. Sin embargo, hay algunas propiedades que son comunes a todos los cuadriláteros, y son las siguientes.
- Tienen cuatro lados.
- Tienen cuatro vértices.
- Tienen dos diagonales.
- La suma de todos los ángulos interiores es 360 °.
A continuación estudiaremos las otras propiedades de los diferentes cuadriláteros en detalle.
Cuadrado
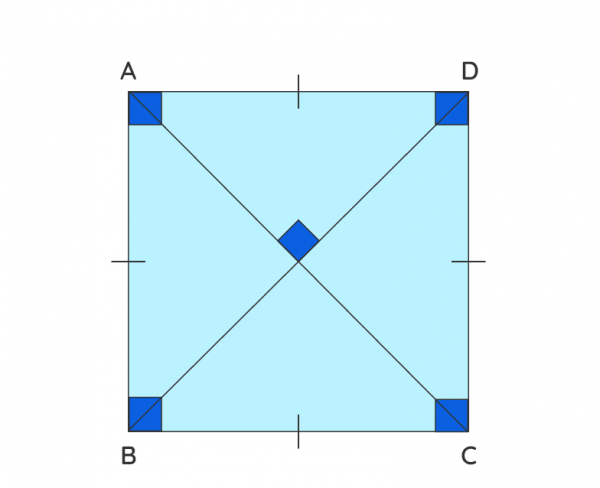
Un cuadrado es un cuadrilátero con cuatro lados iguales y cuatro ángulos rectos.
Estos poseen:
- Cuatro lados iguales AB = BC = CD = DA
- Cuatro ángulos rectos ∠ A = ∠B = ∠C = ∠D = 90 °
- Dos pares de lados paralelos AB ∥ DC y AD ∥ BC
- Dos diagonales iguales AC = BD
- Diagonales que son perpendiculares entre sí AC ⊥ BD
- Diagonales que se bisecan entre sí.
Rectángulo
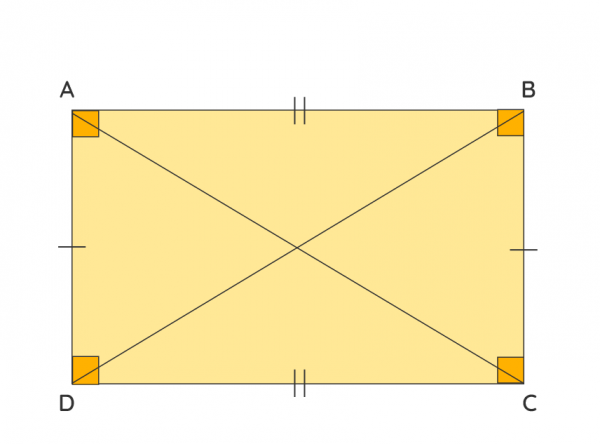
Un rectángulo es un cuadrilátero con dos pares de lados opuestos iguales y paralelos y cuatro ángulos rectos.
El mismo posee:
- Dos pares de lados paralelos AB ∥ DC y AD ∥ BC
- Cuatro ángulos rectos ∠A = ∠B = ∠C = ∠D = 90°
- Lados opuestos de igual longitud AB = DC y AD = BC
- Dos diagonales iguales AC = BD
- Diagonales que se bisecan entre sí.
Paralelogramo
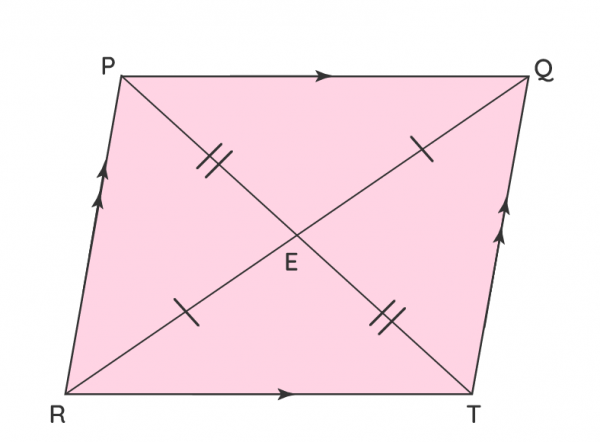
Un paralelogramo es un cuadrilátero en el que ambos pares de lados opuestos son paralelos.
El mismo tiene:
- Dos pares de lados paralelos PQ ∥ RT y PR ∥ QT
- Lados opuestos de igual longitud PQ = RT y PR = QT
- Ángulos opuestos que son iguales ∠P = ∠T y ∠Q = ∠R
- Dos diagonales que se bisecan.
Trapecio
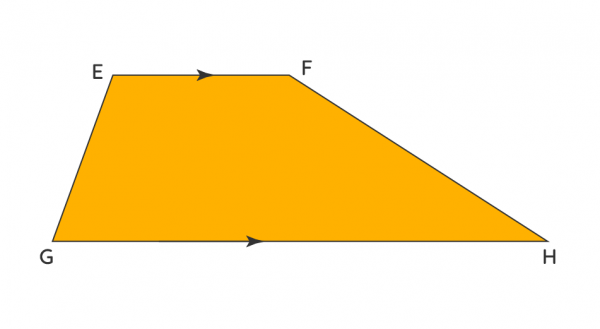
Un trapecio es un cuadrilátero en el que un par de lados opuestos es paralelo.
- Los lados que son paralelos entre sí se llaman bases.
- En la figura anterior, EF y GH son las bases.
- Los lados que no son paralelos entre sí se llaman piernas.
- En la figura anterior, EG y FH son piernas.
No hay nada especial en los lados, ángulos o diagonales de un trapecio. Pero si los dos lados opuestos no paralelos tienen la misma longitud, entonces se llama trapecio isósceles. El siguiente cuadrilátero XYZW es un trapecio isósceles, en el que los catetos son iguales, es decir, WX = ZY, y las diagonales también son iguales, es decir, XZ = WY.
Rombo
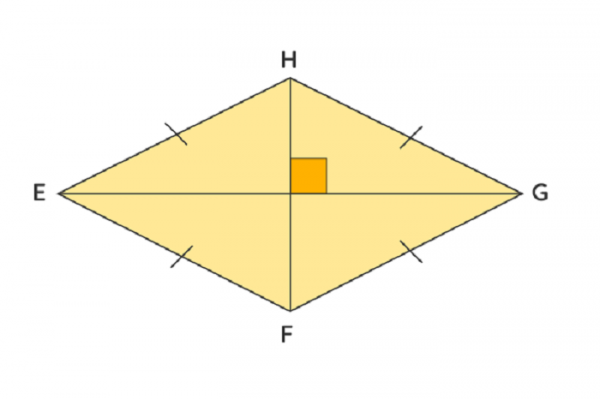
Un rombo es un cuadrilátero con cuatro lados iguales.
El mismo tiene:
- Dos pares de lados paralelos EH ∥ FG y EF ∥ HG
- Cuatro lados iguales EH = HG = GF = FE
- Ángulos opuestos que son iguales ∠E = ∠G y ∠H = ∠F
- Diagonales que son perpendiculares entre sí EG ⊥ HF
- Diagonales que se bisecan entre sí.
Cometa
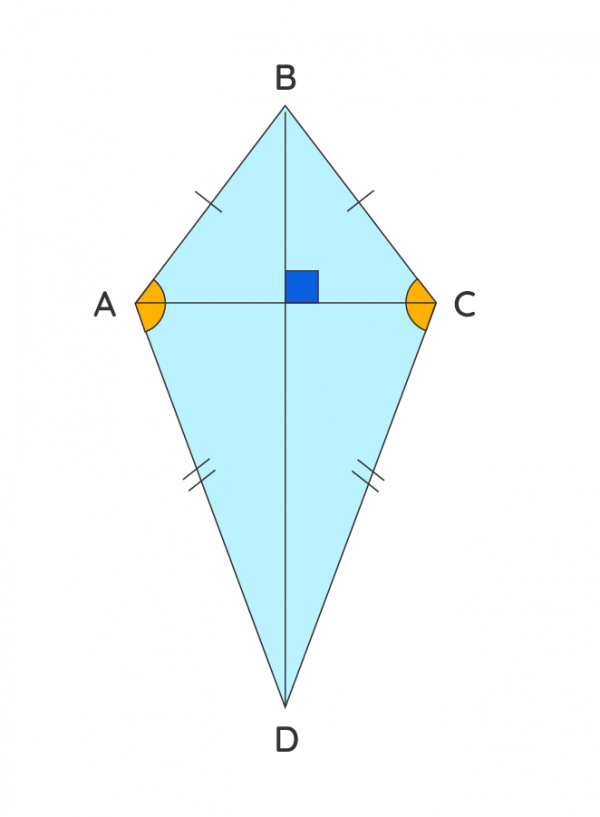
Una cometa es un cuadrilátero en el que dos pares de lados adyacentes son iguales.
Una cometa tiene:
- Dos pares de lados adyacentes iguales AB = BC y CD = DA
- Un par de ángulos opuestos (que son obtusos) que son iguales ∠A = ∠C
- Diagonales que son perpendiculares entre sí AC ⊥ BD
- Una diagonal más larga divide en dos la diagonal más corta.
Área de los cuadriláteros
El área del cuadrilátero es el espacio total ocupado por la figura. A continuación les mostraremos las fórmulas del área para los diferentes cuadriláteros existentes:
- Área de un paralelogramo = base x altura
- Área de un rectángulo = largo x ancho
- Área de un cuadrado = lado x lado
- Área de un rombo = (1/2) x Diagonal 1 x Diagonal 2
- Área de una cometa = 1/2 x Diagonal 1 x Diagonal 2
Perímetro de los cuadriláteros
El perímetro es la distancia total cubierta por el límite de una forma bidimensional. Como sabemos que el cuadrilátero tiene cuatro lados, el perímetro de cualquier cuadrilátero será igual a la suma de la longitud de los cuatro lados. Si ABCD es un cuadrilátero, el perímetro de ABCD es:
Perímetro = AB + BC + CD + AD
- Cuadrado = 4 x lado
- Rectángulo = 2 (largo + ancho)
- Paralelogramo = 2 (Base + Lateral)
- Rombo = 4 x lado
- Cometa = 2 (a + b), a y b son pares adyacentes
Puntos importantes sobre los cuadriláteros
- Un cuadrilátero es un trapecio si 2 de sus lados son paralelos entre sí.
- Un cuadrilátero es un paralelogramo si 2 pares de lados son paralelos entre sí.
- Los cuadrados y los rectángulos son tipos especiales de paralelogramos. A continuación se presentan algunas propiedades especiales:
- Todos los ángulos internos son rectos (90 grados).
- Cada figura contiene 4 ángulos rectos.
- Los lados de un cuadrado tienen la misma longitud (todos los lados son congruentes)
- Los lados opuestos de un rectángulo son iguales.
- Los lados opuestos de un rectángulo y un cuadrado son paralelos.
- Un cuadrilátero es un rombo, si todos los lados tienen la misma longitud y 2 pares de lados son paralelos entre sí.
- Una cometa es un tipo especial de cuadrilátero, en el que 2 pares de lados adyacentes son iguales entre sí.
Ejercicios de cuadriláteros
Ejercicio 1: ¿Cuál es la base de un rombo, si su área es de 40 unidades cuadradas y la altura es de 8 unidades?
Solución: Dado que el área es de 40 unidades cuadradas y la altura de 8 unidades.
Área del rombo = Base × Altura
40 = Base × 8
Base = 40/8 = 5 unidades
Ejercicio 2: Si 15 metros y 6 metros son longitudes diagonales de una cometa, ¿cuál es su área?
Solución: Dado, diagonal 1 = 15 metros y diagonal 2 = 6 metros. Entonces, el área simplemente se calcula como, (1/2) (15 × 6) = 45 m2.
Ejemplo 3: Encuentra el perímetro del cuadrilátero con lados de 5 cm, 7 cm, 9 cm y 11 cm.
Solución: Dado, los lados del cuadrilátero son 5 cm, 7 cm, 9 cm y 11 cm.
Por lo tanto, el perímetro del cuadrilátero es:
P = 5 cm + 7 cm + 9 cm + 11 cm = 32 cm