Actualizado 26 agosto, 2021
Una ecuación que tiene solo una operación matemática con dos números, es un caso simple de sumar, restar, multiplicar, dividir y encontrar su respuesta. Pero, ¿qué pasa cuando hay varios números y diferentes operaciones? Tal vez necesite dividir y multiplicar, o sumar y dividir. ¿Que haces entonces? Afortunadamente, las matemáticas son una disciplina basada en la lógica. Como suele ocurrir, existen algunas reglas sencillas a seguir que le ayudarán a determinar el orden en el que realizar el cálculo. Estas llevan el nombre de jerarquía de las operaciones y a continuación les dejaremos una gran cantidad de información para que puedan aprender todo acerca de ellas, así como también para encontrar ejemplos y ejercicios.
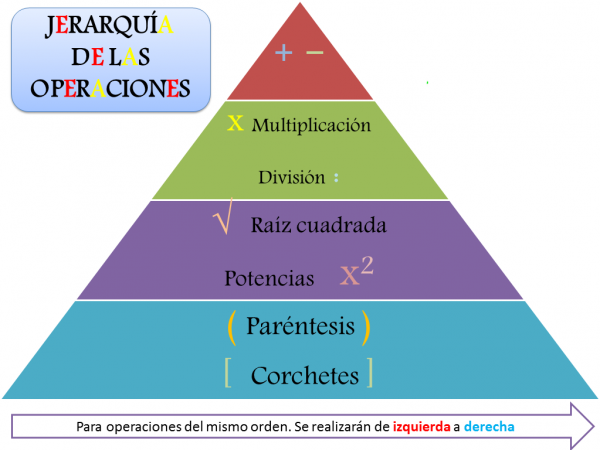
¿Qué es la jerarquía de operaciones?
Las operaciones son cosas como suma, resta, multiplicación y división, por lo que, cuando sumas dos números, estás realizando la operación de suma entre ellos. De manera similar, cuando multiplica números, estás realizando la operación de multiplicación. La jerarquía de operaciones es la regla que determina qué operaciones deben realizarse primero cuando hay varias dentro de la misma ecuación.
El orden de las operaciones es como las reglas gramaticales del lenguaje matemático. Explica cómo interpretar una ecuación para que signifique lo que se supone que significa. La jerarquía de operaciones dice que se deben realizar en el siguiente orden: paréntesis, exponentes, multiplicación, división, suma y resta.
Paréntesis
Cuando hay paréntesis, lo que hay dentro debe hacerse primero. Es posible que el contenido entre paréntesis también deba desglosarse de acuerdo con el orden de las operaciones. Incluso es posible tener paréntesis entre paréntesis. En casos como este, trabaje de adentro hacia afuera.
Exponentes
Si hay exponentes en la ecuación, estos se harían a continuación.
Multiplicación y división
La multiplicación y la división se pueden hacer juntas. En otras palabras, no importa si primero hace la división o la multiplicación, pero deben hacerse después de los paréntesis y exponentes y antes de la suma y la resta.
Suma y resta
La suma y la resta también funcionan juntas. Primero puede restar o puede sumar primero. Son parte del mismo paso, sin embargo, solo se pueden hacer después de los elementos entre paréntesis, exponentes y cualquier multiplicación y división.
Cómo aplicar la jerarquía de operaciones
Si se le pide que simplifique algo como «4 + 2 × 3», la pregunta que surge naturalmente es «¿De qué manera hago esto? ¡Porque hay dos opciones!» Podría sumar primero: 4 + 2 × 3 = (4 + 2) × 3 = 6 × 3 = 18 o podría multiplicar primero: 4 + 2 × 3 = 4 + (2 × 3) = 4 + 6 = 10
¿Cuál es la respuesta correcta? Parece que la respuesta depende de cómo se mire el problema. Pero no podemos tener este tipo de flexibilidad en matemáticas; las matemáticas no funcionarán si no puede estar seguro de la respuesta, o si se puede calcular exactamente la misma expresión para que pueda llegar a dos o más respuestas diferentes.
Para eliminar esta confusión, tenemos algunas reglas de precedencia, establecidas al menos desde el siglo XVI, llamadas «jerarquía de operaciones«. Las «operaciones» son suma, resta, multiplicación, división, exponenciación y agrupación; el «orden» de estas operaciones establece qué operaciones tienen prioridad (son atendidas) antes que otras operaciones.
Una técnica común para recordar el orden de las operaciones es la abreviatura en inglés (o, más propiamente, el «acrónimo») «PEMDAS«. Esta frase representa y ayuda a recordar el orden de Parentheses, Exponents, Multiplication and Division, Addition and Subtraction (que en español sería paréntesis, exponentes, multiplicación y división, y suma y resta). Esta lista le indica los rangos de las operaciones: los paréntesis superan a los exponentes, que están por encima de la multiplicación y la división (pero la multiplicación y la división están en el mismo rango), y la multiplicación y la división superan a la suma y la resta (que están juntas en el rango inferior). En otras palabras, la precedencia es:
- Paréntesis (simplifica dentro de ellos)
- Exponentes
- Multiplicación y división (de izquierda a derecha)
- Suma y resta (de izquierda a derecha)
Cuando tienes un montón de operaciones del mismo rango, simplemente operas de izquierda a derecha. Por ejemplo, 15 ÷ 3 × 4 no es 15 ÷ (3 × 4) = 15 ÷ 12, sino más bien (15 ÷ 3) × 4 = 5 × 4, porque, yendo de izquierda a derecha, se llega a la división firmar primero.
Reglas de orden en la jerarquía de operaciones
Las reglas de la jerarquía de operaciones comienzan con el paréntesis y luego se realizan operaciones en los exponentes o potencias. A continuación, realizamos operaciones de multiplicación o división de izquierda a derecha. Finalmente, las operaciones de suma o resta se realizan de izquierda a derecha.
- Las operaciones entre paréntesis deben realizarse primero.
- Luego, resuelve los exponentes de la expresión.
- Muévase de izquierda a derecha y realice la multiplicación o división, lo que ocurra primero.
- Muévase de izquierda a derecha y realice sumas o restas, lo que ocurra primero.
La presencia de varios paréntesis suele causar confusión. Si no sabemos qué paréntesis resolver primero, podría dar lugar a una respuesta incorrecta. Ahora aprenderemos a resolver esta expresión con varios corchetes.
4 + 3 [8-2 (6-3)] ÷ 2
Comenzaremos trabajando desde el interior de los corchetes. Primero resolveremos el paréntesis más interno y luego nos moveremos hacia afuera.
- Comenzando con 6 – 3 = 3, obtenemos: 4 + 3 [8 – 2 (3)] ÷ 2
- Luego, multiplicando 2 (3) = 6 o 2 × 3 = 6, obtenemos: 4 + 3 [8 – 6] ÷ 2
- Queda un corchete, [8 – 6] = 2, obtenemos: 4 + 3 [2] ÷ 2
- Resolviendo 3 [2] o 3 × 2 = 6, tenemos: 4 + 6 ÷ 2
- Podemos observar que todas las expresiones entre paréntesis están resueltas. Basado en PEMDAS, sabemos que la división viene a continuación, por lo tanto, 6 ÷ 2 = 3, es decir, 4 + 3. Y por último, la suma 4 + 3 = 7.
Ejemplos
Ejemplo 1: ¿Cómo se resuelve 3 + 6 × 2?
Multiplicación antes de la suma:
Primero 6 × 2 = 12, luego 3 + 12 = 15
Ejemplo 2: ¿Cómo te ejercitas (3 + 6) × 2?
Primero los paréntesis:
Primero (3 + 6) = 9, luego 9 × 2 = 18
Ejemplo 3: ¿Cómo se resuelve 12/6 × 3/2?
La multiplicación y la división se clasifican por igual, así que solo ve de izquierda a derecha:
Primero 12/6 = 2, luego 2 × 3 = 6, luego 6/2 = 3
Ejemplo 4: ¿Cómo se resuelve 3 + 6 × 2 4 × (3 + 2)?
Debes hacer la operación, primero dentro de los corchetes, 3 + 2, luego multiplicar la respuesta por 4.
3 + 2 = 5.
4 × 5 = 20
Si ignoraste los corchetes e hiciste el cálculo de izquierda a derecha 4 × 3 + 2 obtendrás 14. Puedes ver cómo los corchetes marcan la diferencia en la respuesta.
Ejercicios para practicar
Ejercicio 1: 3 ^ 2 + 5 =?
Resolución:
Primero debes calcular la potencia, antes de poder sumar 5.
3 ^ 2 = 3 × 3 = 9
9 + 5 = 14
Ejercicio 2: 6 ÷ 2 + 7 × 4 =?
Resolución:
Primero debes hacer la división y la multiplicación, pero tienes una de cada una.
Empiece desde la izquierda y trabaje hacia la derecha, lo que significa que empiece con 6 ÷ 2 = 3. Luego haga la multiplicación, 7 × 4 = 28.
Su cálculo ahora es 3 + 28. Completa el cálculo de la suma para encontrar la respuesta, 31.
Ejercicio 3: 4 + 6 – 7 + 3 =?
Resolución:
Empiezas por la izquierda y avanzas hacia el otro lado.
4 + 6 = 10
10 – 7 = 3
3 + 3 = 6
La respuesta es 6.
Ejercicio 4: 4 + 8 ^ 2 × (30 ÷ 5) =?
Resolución:
Comience con el cálculo dentro de los corchetes: 30 ÷ 5 = 6
Esto le da 4 + 8 ^ 2 × 6 =?
Luego calcule los pedidos, en este caso el cuadrado de 8.
8 ^ 2 = 64. Tu cálculo ahora es 4 + 64 × 6
Luego muévete a la multiplicación 64 × 6 = 384
Finalmente realiza la suma. 4 + 384 = 388
La respuesta es 388.