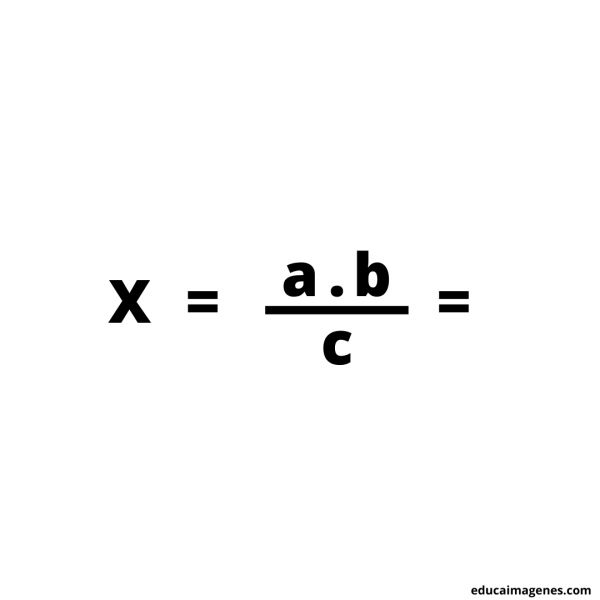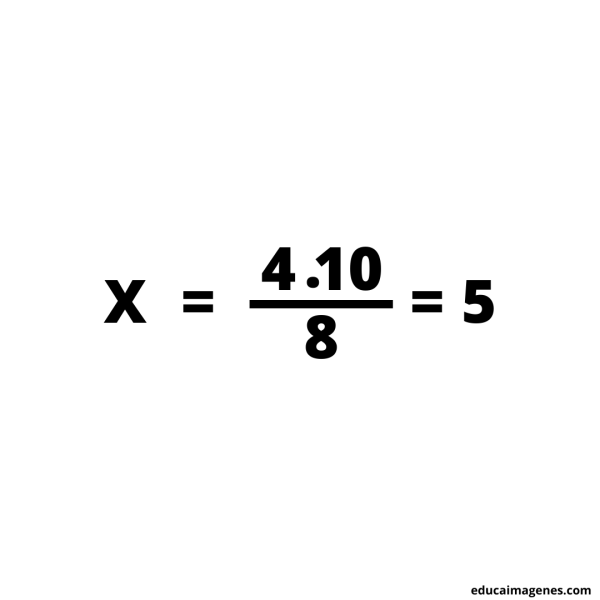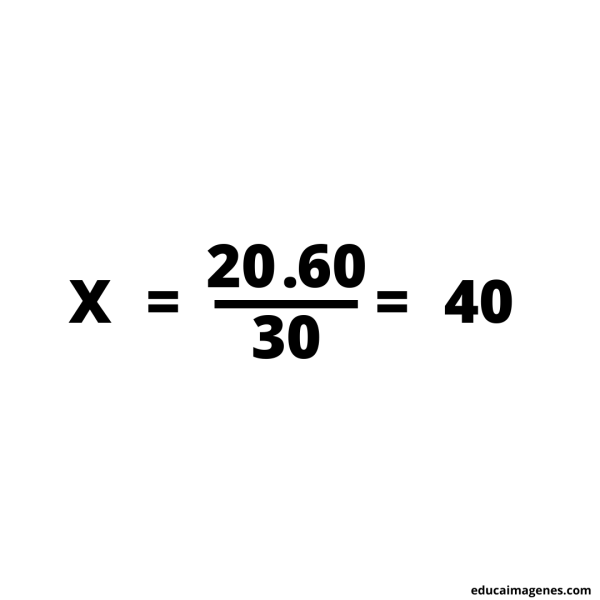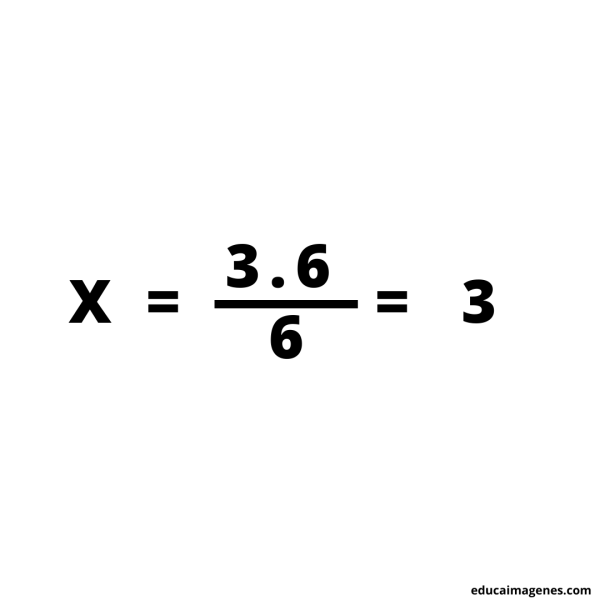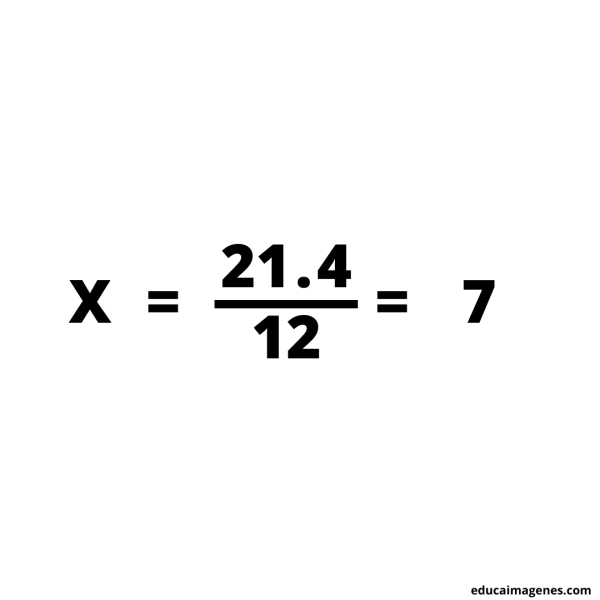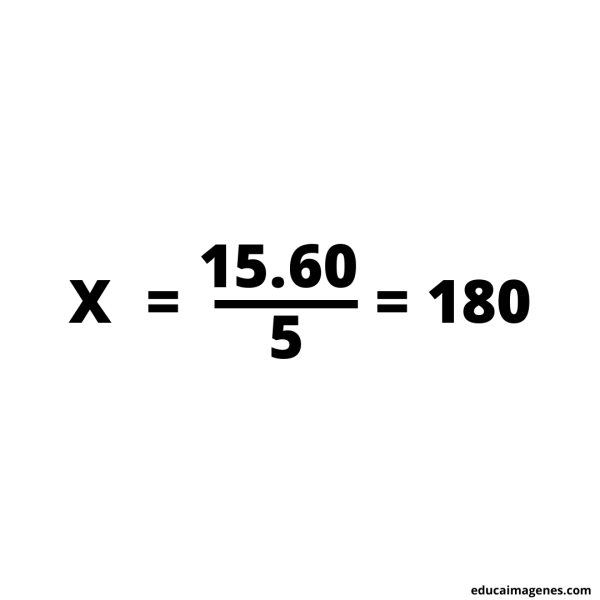Actualizado 19 septiembre, 2022
En esta ocasión, hemos decidido dedicarle, un posteo exclusivo a la regla de tres inversa y a la proporcionalidad inversa. Si estás necesitando ayuda para comprender o necesitas practicar sobre estos temas, estás en lugar indicado. Sigue leyendo y encuentra toda la información que precisas.
¿Qué son las magnitudes inversamente proporcionales?
Definiremos las magnitudes inversamente proporcionales como aquellas que, si al aumentar una, la otra disminuye en la misma proporción. Esto se da en dos momentos, uno de ellos es que cuando multiplicamos a una de ellas por un número, la otra queda dividida por el mismo número, por otro lado, si dividimos una de ellas por un número, la otra queda multiplicada por ese mismo número.
De aquí surge el nombre magnitudes proporcionales inversas, ya que al aumentar una magnitud, la otra disminuye y viceversa.
Por ejemplo: Un tren tarda en recorrer cierta distancia 10 horas, yendo a 50 km/hora; pero si la velocidad aumenta a 100 km/hora, el tren tardará 5 horas en recorrer esa misma distancia. Esto quiere decir que cuando se aumenta al doble la velocidad (de 50km/hora a 100 km/hora), el tiempo disminuye a la mitad (pasando de 10 horas a 5 horas). En cambio, si disminuimos la velocidad del tren a 25 km/hora, ahora tardará en recorrer la misma distancia el doble de tiempo, es decir 20 horas.
¿Cómo aplicar la regla de tres inversa?
En la regla de tres clásica se multiplica de manera cruzada, pero al ser una regla de tres inversa, la multiplicación se hace de manera horizontal.
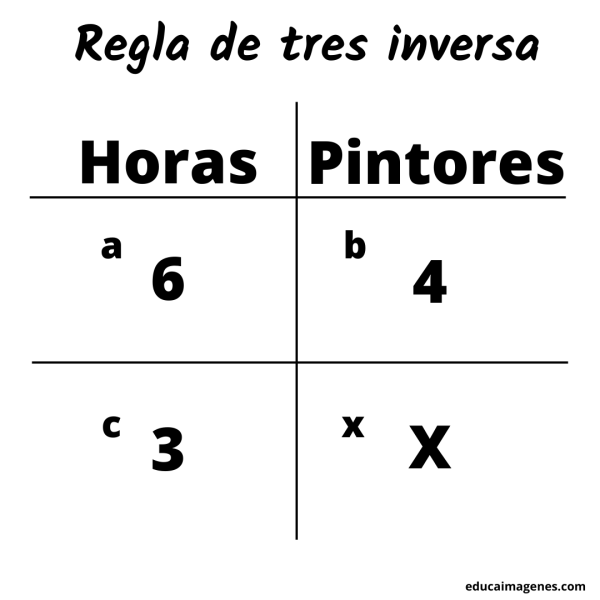
Ejemplo: si 4 pintores tardaron 6 horas en pintar una casa, cuantos pintores se necesitarían para pintar la misma casa pero en 3 horas.
Para aplicar la regla de tres inversa, primero debemos plasmar los datos.
Una vez que hemos plasmados los datos en una tabla, debemos utilizar la fórmula de la imagen.
Luego debemos colocar los datos en el lugar que correspondan. Y así resolver el cálculo.
Entonces encontramos que para pintar una casa en 3 horas, necesitaremos 8 pintores.
¿Cómo resolver problemas de proporcionalidad inversa?
Los problemas de proporcionalidad inversa se pueden resolver de dos maneras:
El primero es con la regla de tres inversa que mencionamos anteriormente. Primero debemos hallar los datos que nos brinda el problema.
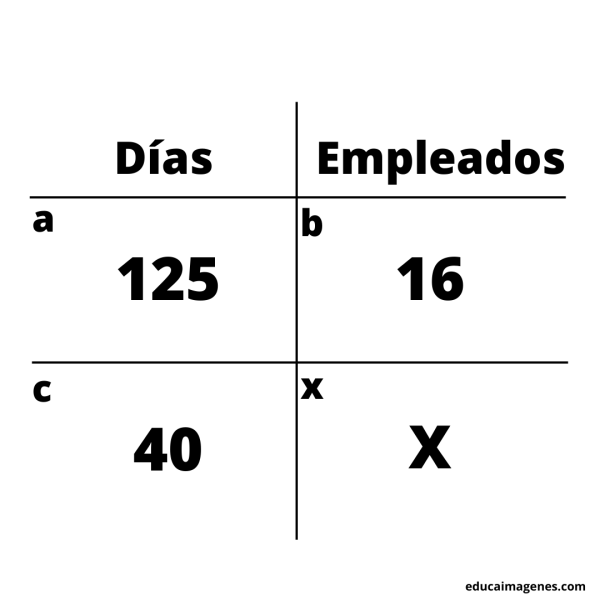
Ejemplo: José reparte mercadería, teniendo 16 empleados, tardan 125 días en repartir el total de la mercadería. ¿Cuántos empleados se necesitan para repartir la mercadería total en un plazo de 40 días?
En este caso podemos observar que teniendo 16 empleados tarda 125 días en repartir la mercadería. La incógnita está en cuantos empleados necesita para repartir la mercadería en 40 días. Se plantea de la siguiente manera.
Luego se aplica la fórmula de regla de tres inversa. Y se obtiene el resultado.
La segunda manera de resolver un problema de magnitudes inversamente proporcionales es con la reducción a la unidad. Este método se basa en averiguar el valor de la segunda magnitud, si la primera vale 1. Luego, con esta información, los demás valores de la segunda magnitud se pueden obtener fácilmente, a partir de la primera magnitud.
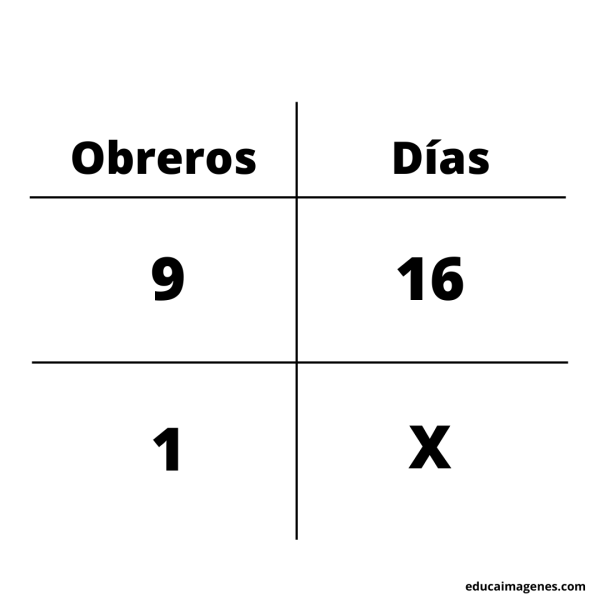
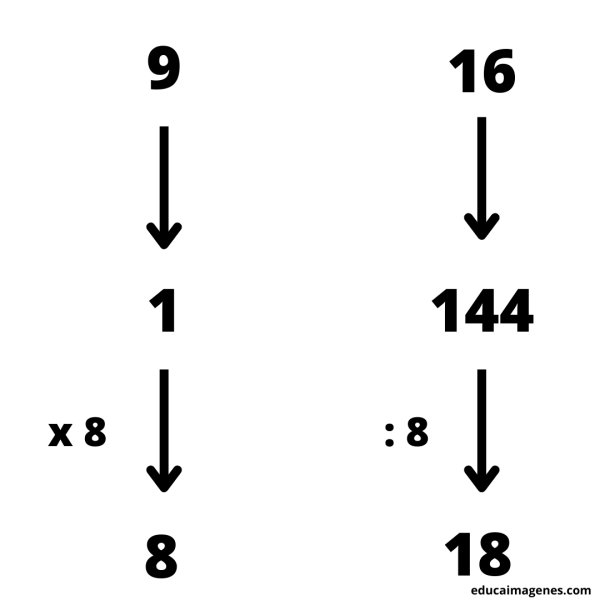
Ejemplo: 9 obreros tardan 16 días en reparar una casa. ¿Cuántos días tardarán en realizar el mismo trabajo, 8 personas?
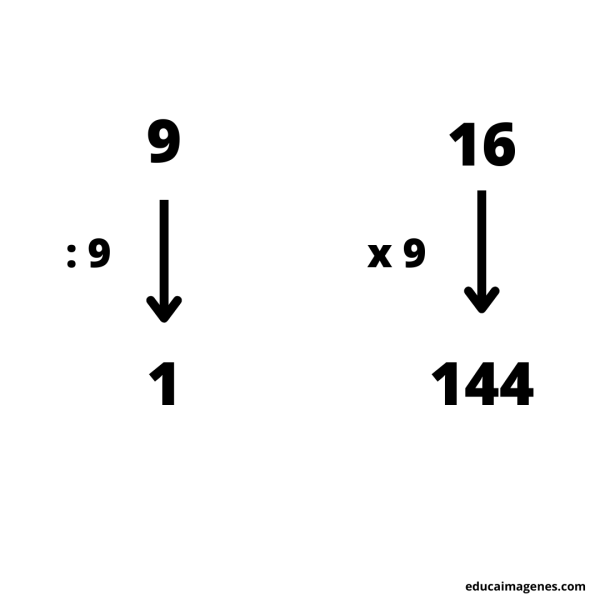
Primero debemos averiguar cuanto tarda un obrero en realizar la reparación de una casa.
Una vez obtenido el dato de cuanto tardará un obrero en realizar la reparación de la casa. Tendremos que averiguar cuantos días tardarían 8 obreros en reparar la casa.
Ejemplos de regla de tres inversa
A continuación hallarás ejemplos de regla de tres inversa para que puedas comprender como se aplica esta regla a cada problema planteado.
Ejemplo 1
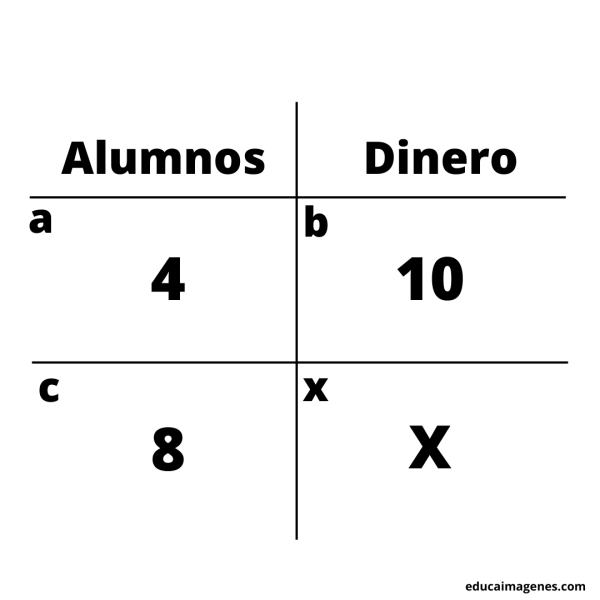
Un grupo de alumnos, por el cumpleaños de su maestra, organizaron hacerle un regalo. En un principio eran 4 compañeros e iban a poner $10 cada uno, pero luego de unos días terminaron siendo 8 alumnos, los que se sumarán al regalo para la maestra. ¿Cuánto dinero deberá poner cada uno de ellos?
Primer paso: plantear la situación.
Segundo paso: colocar en donde corresponde cada dato. Utilizando la fórmula.
Tercer paso: resolver el cálculo.
Ejemplo 2
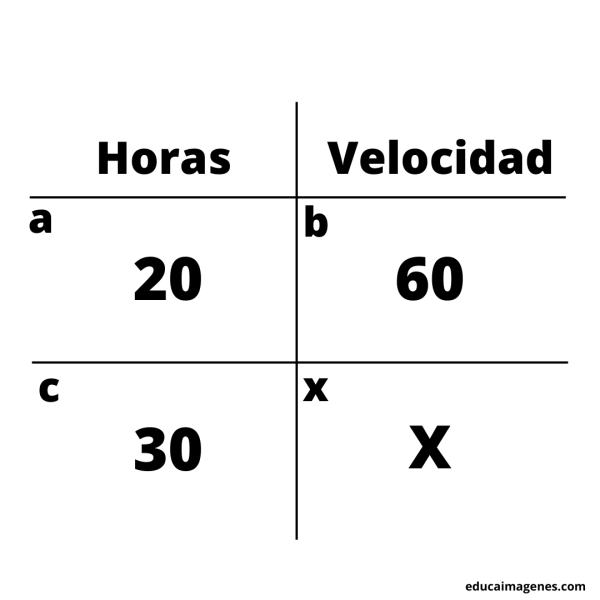
Un camionero tarda 20 horas en llegar a destino, conduciendo a una velocidad de 60 km/h. Si puede tardarse 30 horas como máximo en llegar, ¿Cuál es la mínima velocidad a la que puede conducir para llegar al destino en el tiempo máximo?
Primer paso: plantear la situación.
Segundo paso: colocar en donde corresponde cada dato. Utilizando la fórmula.
Tercer paso: resolver el cálculo.
Ejemplo 3
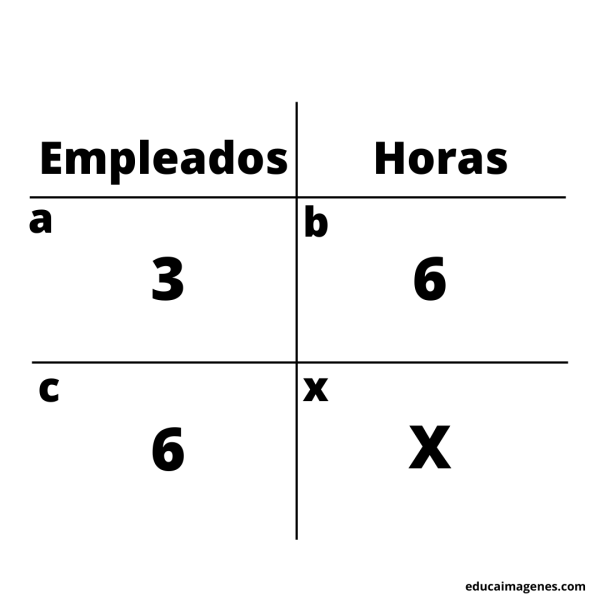
En un hospital hay 3 empleados de mantenimiento, ente todos realizan todas las tareas de limpieza y reparación en 6 horas. Si contratarán 3 empleados más, ¿en cuánto tiempo realizarán las tareas que anteriormente se realizaban en 6 horas?
Primer paso: plantear la situación.
Segundo paso: colocar en donde corresponde cada dato. Utilizando la fórmula.
Tercer paso: resolver el cálculo.
Ejemplo 4
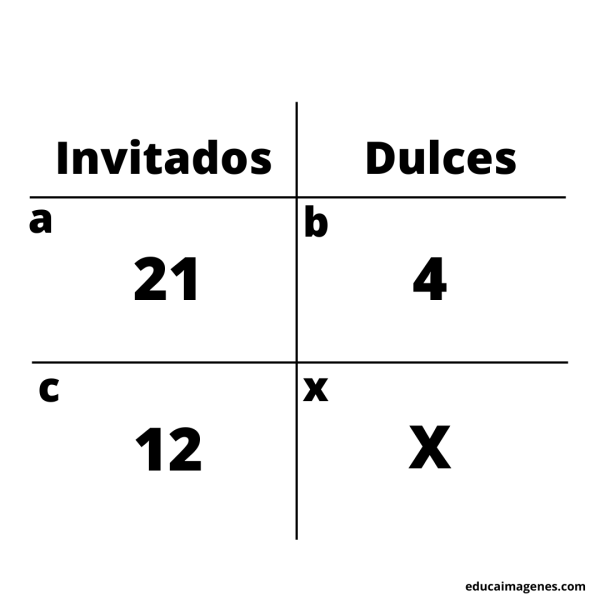
Un compañero de clases festejará su cumpleaños y en el souvenir quiere colocar 4 dulces en cada bolsa. En el curso son 21 compañeros, pero a la fiesta solo han asistido 12, por lo cual, el cumpleañero decide repartir los dulces de manera equitativa a quienes fueron a su festejo. ¿Cuántos dulces le tocará a cada invitado?
Primer paso: plantear la situación.
Segundo paso: colocar en donde corresponde cada dato. Utilizando la fórmula.
Tercer paso: resolver el cálculo.
Ejemplo 5
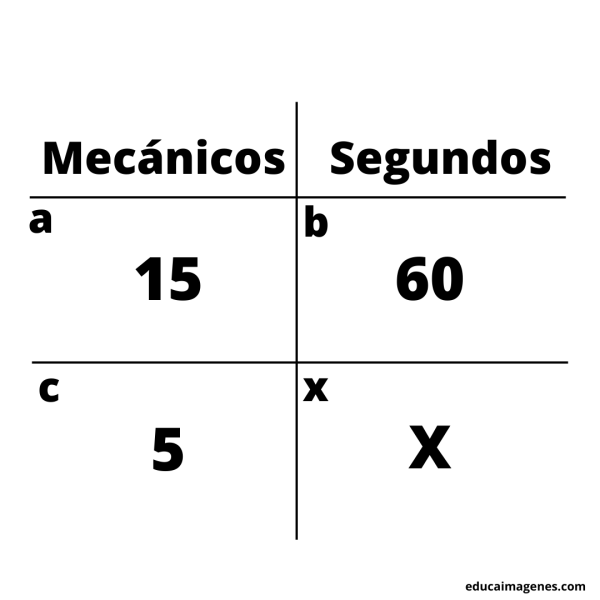
En un equipo de la Fórmula 1, hay 15 mecánicos que pueden realizar la revisión del auto en 60 segundos. ¿Cuántos segundos tardarán en realizar el mismo trabajo 5 mecánicos?
Primer paso: plantear la situación.
Segundo paso: colocar en donde corresponde cada dato. Utilizando la fórmula.
Tercer paso: resolver el cálculo.
Problemas con regla de tres inversa
En este apartado, para afianzar el conocimiento adquirido, te brindaremos problemas con regla de tres inversa, para que practiques y comprendas bien este tema.
Problema 1
Un ciclista tarda 20 segundos en realizar 100 metros planos a una velocidad de 5 m/s. ¿En cuanto tiempo realizará el recorrido si incrementa su velocidad a 8 m/s?
Problema 2
Una empresa de empaquetado posee 3 máquinas que realizan los empaquetados, las mismas realizan un pedido diario de 2400 empaquetados. En temporada alta, el pedido diario se incrementa a 5600 paquetes. ¿Cuántas máquinas empaquetadoras deberán comprar para cumplir con los pedidos requeridos?
Problema 3
Cinco operarios tardan 9 horas en revisar el motor de todos los trenes de la estación. ¿Cuánto se tardaría en realizar el mismo trabajo si se contratan a dos operarios más?
Problema 4
Una familia de 12 integrantes han recaudado $1800 para los gastos de vacacionar 9 días en Cancún, en los que se incluye realizar excursiones y cenar en distintos restaurantes todas las noches. Si por distintos motivos viajarán solo 6 integrantes de la familia, ¿Cuántos días podrán quedarse en Cancún con el dinero recaudado?
Problema 5
Tres amigos han comprado comida para comer durante 8 días en sus vacaciones, sin embargo, se ha sumado otro amigo más a último momento. ¿Cuánto tiempo podrán alimentarse con la comida comprada los cuatro amigos?
Problema 6
Un grifo con un determinado caudal tarda 30 minutos en llenar un depósito. ¿Cuántos minutos tardaría en llenarse el depósito con 3 grifos con el mismo caudal?
Problema 7
Tres trabajadores recolectan 100 naranjas en 5 horas. Uno de ellos ha sufrido un accidente laboral y no puede continuar con su tarea. Calcular cuánto se tardará en recolectar los 300 naranjas restantes entre los dos trabajadores activos.
Problema 8
Si con 70 Kg tenemos para alimentar a 25 gallinas durante 30 días. Si se mueren 15 gallinas ¿para cuántos días habrá comida suficiente?
Problema 9
Pedro dedica 5 h diarias en su proyecto escolar, lo terminará en seis días. ¿Cuántos día le llevará terminar su proyecto si solamente le dedica 3 h al día?