Actualizado 21 octubre, 2020
Se conoce como fracciones a la representación de las partes de un todo. Es decir si dividimos algo en partes iguales y elegimos una de estas partes, la forma de representarlo es a través de las fracciones. De este modo lo que hacemos es dividir un entero, a cada una de las partes en que se dividió se la llama fracción.
Dentro del mundo de las fracciones podemos encontrar a las fracciones equivalentes. A continuación conoceremos sobre ellas.
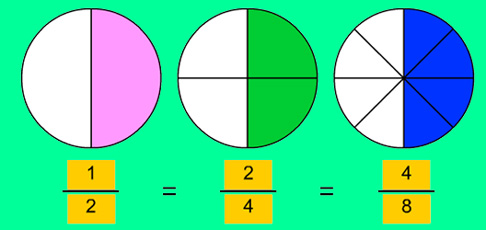
Fracciones
Antes de conocer al detalle las fracciones equivalentes recordaremos que son las fracciones y sus partes.
Tal como detallábamos las fracciones son números que se obtienen luego de dividir un entero en partes iguales. Por ejemplo si tenes la octava parte de una pizza, estamos dividiendo la pizza en ocho partes iguales y solo tomamos una de esas partes (1/8).
Una fracción es representada gráfica y matemáticamente por medio de números, los cuales estarán escritos uno por encima del otro y separados por medio de una línea horizontal que llamaremos raya fraccionaria. Aquellos números que se ubiquen por encima de la raya fraccionara (termino superior) se llaman numeradores y aquellos números que se ubiquen por debajo de la línea fraccionaria (termino inferior) se llaman denominadores.
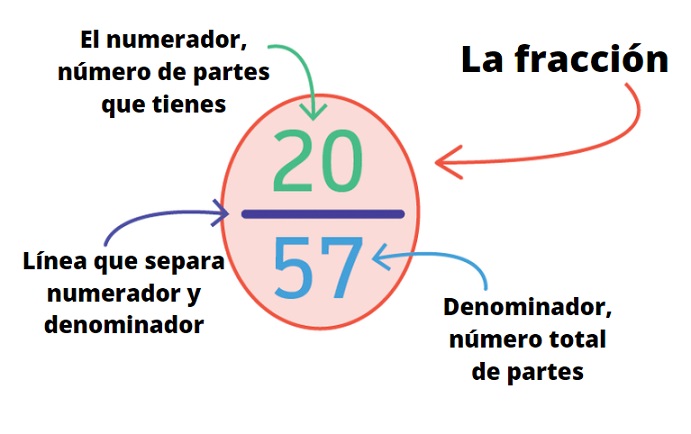
El o los numeradores representan a las partes que se toman de un todo, y el o los denominadores representan al total de las partes en que dividimos al entero, es decir el numerador.
Por ejemplo: Siguiendo con nuestro caso inicial, si tenemos una pizza y la dividimos en ocho partes iguales, cada una de sus partes representa un octavo del total de la pizza. Si comemos cuatro de dichas porciones, podemos afirmar que comimos cuatro octavos de nuestra pizza.
De este modo el ocho es el denominador y siempre será el mismo, lo que cambia es el numerador.
¿Qué son las fracciones equivalentes?
Dos fracciones se consideran equivalentes cuando representan la misma cantidad, es decir el resultado de las divisiones que ambas representan son iguales. Llamamos división cuando dividimos al numerador por el denominador.
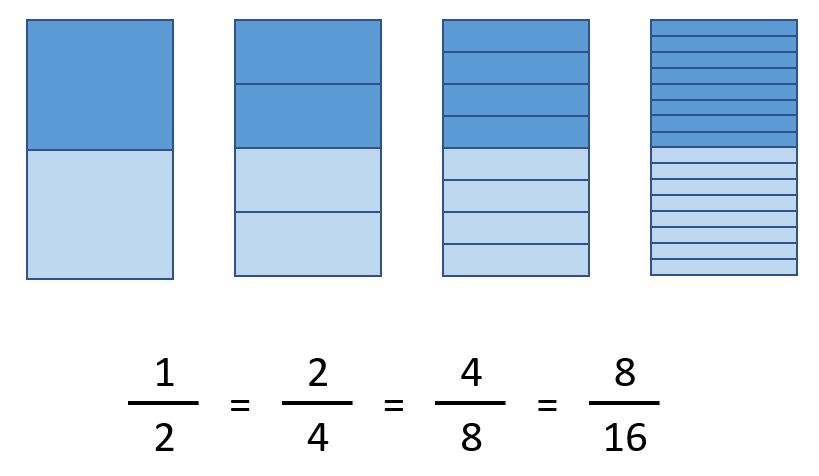
Veamos un ejemplo:
Las fracciones 6/3 (seis tercios) y 8/4 (ocho cuartos) son dos fracciones equivalentes, ya que sus resultados son iguales. Observando la primer fracción si dividimos seis entre tres obtendremos como resultados dos, ahora si miramos la segunda fracción y dividimos ocho entre cuatro también tendremos como resultados dos.
Del mismo modo podremos ver, que si representamos las fracciones como partes iguales de un total, las mismas representarán la misma porción del total.
¿Cómo saber si dos fracciones son equivalentes?
Para determinar si dos fracciones son equivalentes o no, debemos multiplicar el denominador de la primera por el numerador de la segunda y este resultado debe ser igual al resultado de multiplicar el numerador de la primera por el denominador de la segunda. Este método es conocido como método de la cruz.
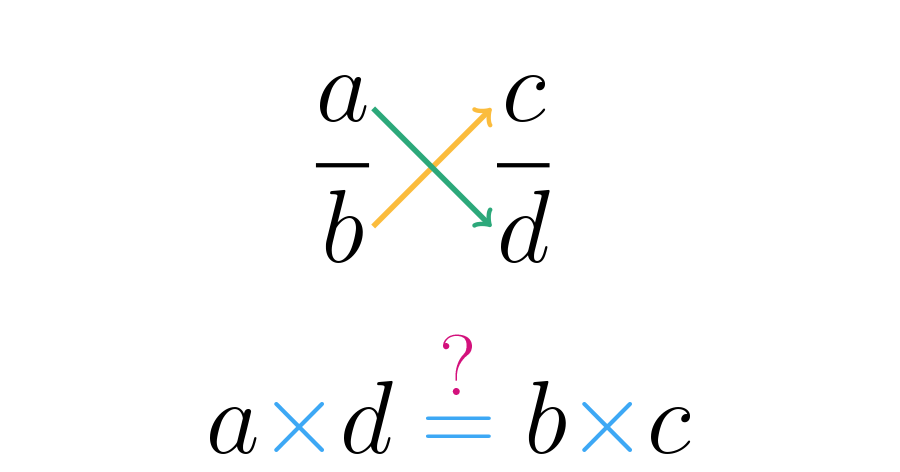
Dos fracciones serán equivalentes cuando los productos del numerador de una y el denominador de la otra son iguales, esto significa que son productos cruzados. Por ejemplos:
Tenemos las fracciones dos quintos (2/5) y la fracción cuatro decimos (4/10), para saber si las mismas son iguales, hacemos el producto cruzado. Es decir:
-Dos por diez: 20
-Cinco por cuatro: 20
Como vemos ambos productos dan el mismo resultado, por lo tanto podemos decir que las fracciones 2/5 y 4/10 son fracciones equivalentes.
¿Cómo encontrar una fracción que sea equivalente a otra?
Para poder encontrar una fracción que sea equivalente de otra, podemos aplicar dos métodos: la multiplicación o la división.
- Método de la multiplicación o proceso de amplificación
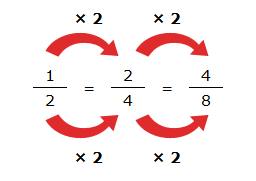
Consiste en multiplicar el denominador y el numerador por el mismo número. De esto modo obtendremos una fracción equivalente pero con un numerador y denominador mayor. Es por este motivo que se lo denomina proceso de amplificación.
Por ejemplo: si partimos de la fracción 1/3 y multiplicamos a ambos términos por el numero tres, obtendremos una fracción más grande que sería: 3/9. De este modo podríamos seguir multiplicando para ampliarla aun más.
- Método de la división o proceso de simplificación
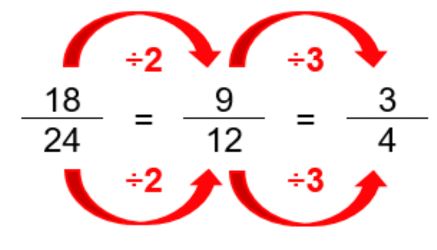
Consiste en dividir el denominador y el numerador por el mismo numero. Hay que tener en cuenta que ambas fracciones deben ser divisibles por dicho numero. Una vez que obtendremos estaremos hallando una fracción que es equivalente pero con un denominador y numerador más pequeño, es por este motivo que se dice que se simplifica.
Por ejemplo: Si partimos de una fracción que es 6/15, dividimos ambos términos por un número que sea divisible por los dos, por ejemplo tres. Como resultado de esta simplificación obtendremos la fracción 2/5.
¿Para que usamos las fracciones equivalentes?
Si obtenemos como resultado de un problema una fracción, entonces podríamos utilizar cualquier fracción que sea equivalente a ella. Pero debemos tener en cuenta que no es lo mismo trabajar con una fracción que tiene grandes números, que con una fracción que tiene pequeños números como por ejemplo 6/3 (seis tercios).
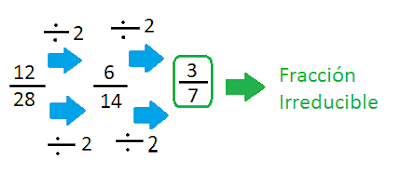
Es por esta razón que por comodidad, siempre nos convendrá elegir la fracción que tiene los números más pequeños, denominada fracción irreductible.
Una fracción es irreductible, cuando el máximo común divisor del numerador y del denominador es el numero uno. Por ejemplo: si estamos analizando la fracción 15/6 (quince sextos) veremos que no es una fracción irreductible, ya que el máximo común divisor de quince y de seis es tres, no uno.
Ahora si analizamos la fracción 5/2 (cinco medios) veremos que si es una fracción irreductible, ya que el máximo común divisor tanto del numerador y del denominador es uno. Por lo tanto llegamos a la conclusión que 15/6 no es una fracción irreductible, pero 5/2 si lo es.
Hay que tener en cuenta que cuando una fracción es irreductible, significa que no existe ningún número que sea divisor común tanto del numerador como del denominador, por consiguiente no existen fracciones equivalentes cuyos números sean más pequeños.
¿Cómo calculamos el máximo común divisor?
Para poder encontrar el máximo común divisor de dos fracciones, debemos descomponer los números y quedarnos con los factores comunes al menor exponente. Cuando el máximo común divisor tanto del denominador como del numerador es uno, implica que ya no hay más factores comunes que puedan simplificarse.
Tipos de fracciones
Existen otros tipos de fracciones además de las equivalentes. Veamos cuales son:
-Fracción propia: Se denomina fracción propia a aquella fracción en la cual el numerador es más chico que el denominador, esto significa que la fracción representa un numero mas pequeño que un entero. Por ejemplo: un medio (1/2), dos sextos (2/6), tres cuartos (3/4).
–Fracción impropia: Se denomina como fracciones impropias a aquellas en las cuales el numerador es un numero más grande que el del denominador, esto significa que estas fracciones representan un número mayor que el entero. Algunos ejemplo: diez medios (10/2), cuatro tercios (4/3), ocho sextos (8/6).
-Fracciones comunes y decimales: Las fracciones comunes son aquellas en donde su denominador no es la unidad seguida de ceros. Por ejemplo: dos quintos (2/5), un septimo (1/7), nueve doceavos (9/12). Por el lado contrario, las fracciones decimales son aquellas fracciones en donde su denominador si es la unidad seguida de ceros. Por ejemplo: cuatro decimos (4/10), dos centésima (2/100), veinte milésimas (20/1000).
-Fracciones mixtas: Se denomina fracciones mixtas a aquellas fracciones que se componen por un número entero y una fracción propia, que se representan juntos o combinados. Por ejemplo: 4 5/2.
–Fracciones homogéneas: Las fracciones homogéneas son aquellas que tienen igual denominador. Si estamos frente al caso en que dos fracciones tienen el mismo denominador positivo entonces la fracción mayor será la que mayor numerador tiene.