Expresiones algebraicas (ejemplos, ejercicios, tipos y simplificación)

Actualizado 28 julio, 2020

Trabajar con expresiones algebraicas consiste en analizar relaciones numéricas en las que una o más cantidades son desconocidas. Estas incógnitas son conocidas como variables o indeterminadas y son representadas por medio de letras.

A continuación conoceremos que son las expresiones algebraicas, sus tipos, simplificación y ejemplos.

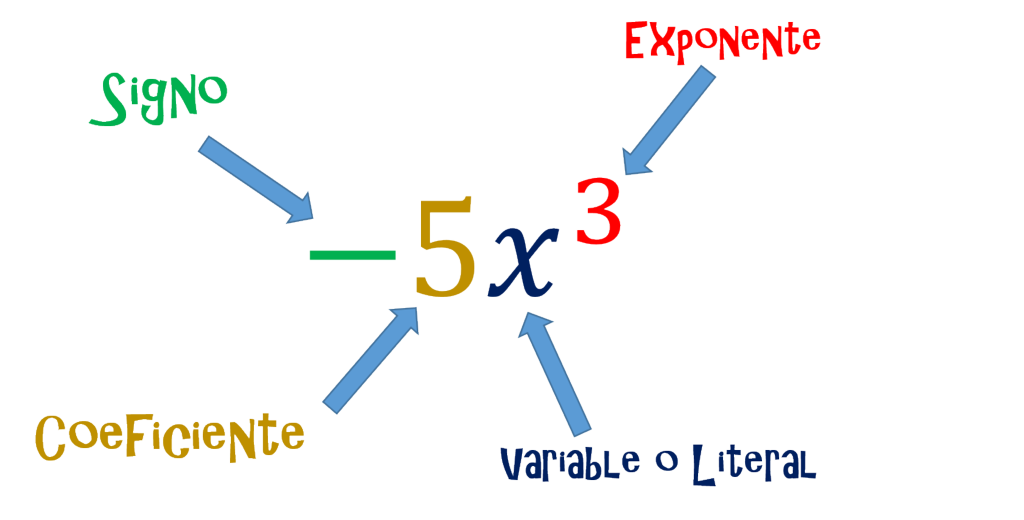
¿Que son las expresiones algebraicas?

Las expresiones algebraicas son las relaciones entre variables y constantes que demuestran una operación entre ellas. Las operaciones que podemos realizar son suma, resta, multiplicación, división y potenciación.

Es importante a la hora de calcular una expresión algebraica, tener en cuenta el orden de las operaciones:

1. Potencias
2. Productos y cocientes
3. Sumas y restas

Una variable e incógnita es una letra que se utiliza para representar un número.  Las letras representan valores que no conocemos y podemos considerarla como generalización de un número.

Por medio de las expresiones algebraicas podemos hallar por ejemplo áreas y volúmenes.

Ejemplo de expresiones algebraicas:

-Longitud de la circunferencia:  L=2\pi r, donde r es el radio de la circunferencia.

-Área del cuadrado: S=l^{2}, donde l es el lado del cuadrado.

-Volumen del cubo: V=a{3}= a³, donde a es la arista del cubo.

Valor numérico de una expresión algebraica

Si en una expresión algebraica  sustituimos las variables por números, lo que tendremos será una expresión numérica. El resultado de esta expresión es lo que se denomina valor numérico de la expresión algebraica para dichos valores de las variables.

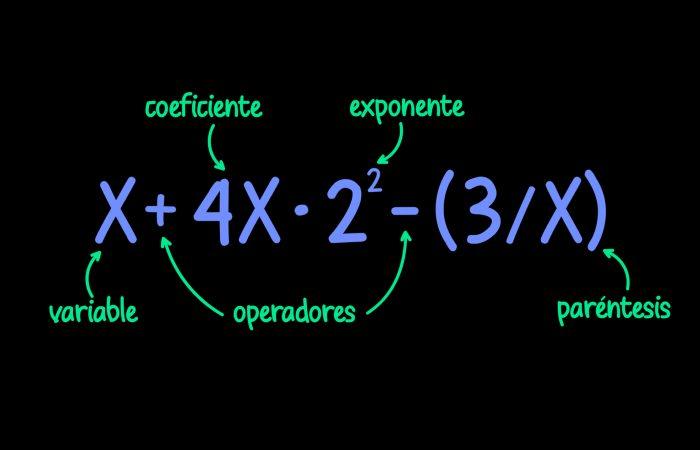
Clasificación de las expresiones algebraicas

Las expresiones algebraicas se clasifican de acuerdo al número de términos que tenga. Las mismas pueden ser:

Monomios

Es aquella expresión que contiene solo un termino. En este tipo de expresión las únicas operaciones que aparecen entre sus variables con la multiplicación y la potencia de exponente natural. Por ejemplo:

1) -13xy

2) 7y⁵z

3) a²b3c

Binomios

Es una expresión algebraica que contiene dos términos. Por ejemplo:

1) x – 9

2) 5x + 10

3) y + ab

Trinomios

Es una expresión algebraica que contiene tres términos. Por ejemplo:

1) -2x – 3y + 8

2) 2×2 + 5x – 5

3) a³ – b² + 2c⁴

Polinomio

Se trata de una expresión algebraica formada por más de un monomio. Por ejemplo:

1) 3x² + 4x + 7x – 1

2) -m² + 3m – m + 7

3) 3a²bc + ab + c + 2

Monomios

Tal como explicamos anteriormente un monomio es una expresión algebraica que solo contiene un termino y en donde las únicas operaciones que se pueden dar entre las variables son la multiplicación y la potencia natural.

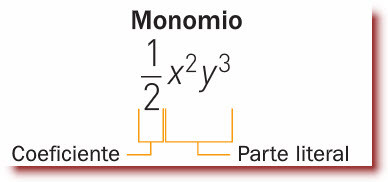
Partes de un monomio

–Coeficiente: es el número que compone el monomio y que multiplica las partes.

–Parte Literal: es el conjunto de variables, ya sea letras como exponentes.

–Grado: el grado de un monomio es la suma de los exponentes  de todas sus letras o variables.

Por ejemplo:

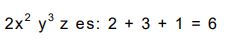
Otro dato a tener en cuenta es que dos monomios son semejantes si sus literales son iguales y dos monomios son opuestos si son semejantes y sus coeficientes son opuestos

Suma y resta de monomios

Para realizar operaciones de suma y resta de monomios, lo primero que debemos realizar es verificar sin son monomios semejantes u opuestos.

En el caso que sean dos monomios semejantes, para realizar la operación debemos sumar o restar los coeficientes y se deja el mismo literal. En cambio si no son semejantes, esta expresión no puede ser expresada de manera más simplificada.

La suma de los monomios da como resultado a otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.

Por ejemplo: Tenemos la siguiente suma de monomios semejantes 3x+6x=9x

Ahora en el caso que sean opuestos no se podrá simplificar: 2x+7y es decir no tendremos como resultado un monomio.

Multiplicación de un número por un monomio

Cuando tenemos el producto de un número por un monomio, obtendremos como resultado otro monomio semejante donde el coeficiente será la multiplicación del coeficiente del monomio por el numero.

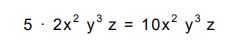
Multiplicación de monomios

El resultado de la multiplicación de monomios será otro monomio que tienen por coeficiente la multiplicación de los coeficientes y donde su parte literal se obtiene multiplicando entre si las partes literales, siempre teniendo en cuenta las propiedades de las potencias.

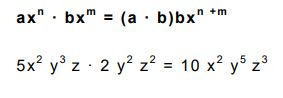
Cociente de monomios

Cuando estamos frente a una operación de cociente de monomios tendremos como resultado otro monomio que tiene como coeficiente la división de los coeficientes  y donde su parte literal la obtendremos del cociente entre las partes literales siempre respetando las propiedades de las potencias.

Potencia de monomios

Frente a operaciones de potencia de monomios, lo que debemos hacer es elevar cada elemento del monomio al exponente de la potencia.

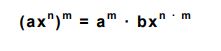
Polinomio

El polinomio es aquella expresión algebraica que posee dos o más términos. Los polinomios pueden ser de una sola variable o de dos variables.

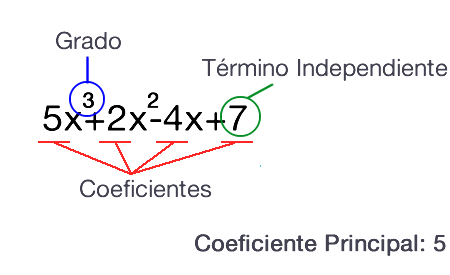
Son expresiones matemáticas que están formadas por un conjunto de números y variables, es decir un polinomio se puede determinar por medio de la presencia de expresos, determinados números  y letras que serán las variables.

Los polinomios de una sola variable son aquellos que poseen una expresión algebraica del siguiente tipo:

En donde an, a n-1…a1, a0 son números que denominaremos coeficientes.

N es un número natural

X es la incógnita o variable

An es el coeficiente principal

A0 es el término independiente

¿Cuál es el grado de un polinomio?

Cuando hablamos de grado de un polinomio, estamos haciendo referencia a un concepto muy directo y que no es muy difícil de entender. Estas expresiones siempre están conformadas por una o más variables, por lo tanto para poder determinar y saber cual es el grado de un polinomio cualquiera, debemos analizar el número de variables que lo componen. En base a este análisis, se decidirá que procedimientos aplicar para definir el grado de un polinomio.

Definiremos como grado de un polinomio P (x) al mayor exponente al que se encuentre elevada la variable x.

Grado de un polinomio de una sola variable

El grado de un polinomio de una sola variable será el mayor exponente que tiene entre todos los termino algebraicos que componen la expresión. No tiene importancia el orden de la expresión ni tampoco los coeficientes numéricos. Veamos algunos ejemplos:

1) 4x² + x + 5 es un polinomio de segundo grado.

2) x² + x⁴ – 3 es un polinomio de cuarto grado.

3) x⁶ – 1 es un polinomio de sexto grado.

4) m² + 2m + 1 = 0 es una ecuación y su polinomio es de segundo grado.

Grado de un polinomio de dos variables

El grado de un polinomio de dos variables será el mayor grado absoluto de todos los términos. Hay que tener en cuenta que los términos se encuentran separados por los signos de mas (+) y menos (-).  Veamos ejemplos:

3) mn²o + 1 es un polinomio de cuarto grado.

4) a² + b² tienen los mismos exponentes y es un polinomio de segundo grado.

5) 4x²y + xy³ + 1 es un polinomio de cuarto grado.

6) 2m² + 2m²n – 3 es un polinomio de tercer grado.

7) 8xy³ + x²y³ es un polinomio de quinto grado.

8) a²bc + 3ac³ + a⁷b³ es un polinomio de décimo grado.

Tipos de polinomios

Existen distintos tipos y clasificaciones de los polinomios, a continuación detallaremos cada uno.

Polinomios según su grado

Tal como explicábamos anteriormente los grados de los polinomios son determinados por los exponentes que aparecen en todos los casos acompañados de las variables. Estos exponentes pueden ser también conocidos como potencia o índice, ya que nos indican cuantas veces se puede multiplicar un numero por si mismo. El mismo es un elemento grafico muy útil para simplificar y logar hacer más visible las multiplicación.

La clasificación de los polinomios según su grado es:

• Polinomios de grado cero o polinomio nulo: son aquellos polinomios en donde sus coeficientes son iguales a cero. Un claro ejemplo de un polinomio nulo sería: P(X) = 0x² +0x.
• Polinomios de primer grado: Se denomina polinomio de primer grado o de grado uno, cuando el mayor exponente que tiene la variable da como resultado igual a uno. Un ejemplo de este tipo de polinomio es: P(X) = 3x + 2.
• Polinomio de segundo grado: Se conoce con este nombre a los polinomios en los cuales el valor más alto que tiene un exponente de variable resulta ser igual a dos, ya sea que se trate del único o el mayor de ellos. Un ejemplo de polinomio de segundo grado es: P(X) 3x + 3 + 8x².
• Polinomio de tercer grado: Esta rama de polinomio son aquellos donde el valor más grande de una variable es igual o mayor a tres. Un claro ejemplo de este tipo de polinomio es: P(X) = x³– 2x² + 3x + 2.

Polinomios según su número de términos

Cuando vemos la expresión gráfica de un polinomio podemos ver que existen diferentes cantidades de números o de variables, estas mismas serán las que determinan a los polinomios según el número de términos que posea. En de este modo que entendemos que cada polinomio recibe un nombre determinado según el número o la cantidad de términos que tenga. La clasificación de los polinomios según su término es:

• Binomios: Tal como lo indica su nombre este tipo de polinomios se caracterizan por tener sólo dos términos. Hay que tener en cuenta que al contar los términos no debemos incluimos ni los signos ni la letra P con la que se inician las expresiones algebraicas, ya que la función de esta ultima es indicar que se trata de un polinomio. Los binomios son comunes en diferentes operaciones matemáticas es por ellos que es necesario reconocerlos muy bien. Un ejemplo de binomio sería: P(X) = 3 + x.
• Trinomios: Este tipo de polinomio son aquellos en los que se pueden apreciar tres monomios, es decir tres términos. Dicho de otro modo, podemos definir a un trinomio la suma de tres expresiones numéricas que pueden ser números únicamente o bien variables. Un ejemplo de trinomio sería: P(X) = 2 + 4x + 9 + 5x²

En los trinomios podemos observas algunos casos diversos como puede ser por ejemplo un trinomio cuadrado perfecto que esta conformado por tres términos pero este es el resultado de elevar al cuadrado un solo binomio. Otro caso que podemos observar también es un trinomio irreducible que es aquel que no se puede factorizar, es decir encerrar en ninguna expresión de menor grado ya sea con números racionales o bien con elementos reales.

• Cuatrinomios: Este tipo de polinomios es uno de los que se consideran más complejos dentro de todas las expresiones algebraicas, además de que no suelen observarse con mucha frecuencia. Se trata de un polinomio en el cual se pueden ver cuatro términos, los cuales pueden formarse tanto por números como por variables. Un ejemplo de este tipo de polinomio sería: P(X) = x³ + 6x² + 12x + 8.

Otros tipos de polinomios

Podemos encontrar otros tipos de polinomios que no se encuadran dentro de las clasificaciones anteriores. Los mismos son:

• Polinomio Homogéneo: Reciben este nombre los polinomios en los cuales se puede apreciar que todos los términos o los monomios tienen el mismo grado. Un claro ejemplo: P(X) = 3x² + 2xy.
• Polinomio Heterogéneo: Es aquel polinomio en el cual no todos sus términos tienen el mismo grado. Por ejemplo: P(X) = 3x⁴+2x³ – 3
• Polinomio Completo: Se conoce como polinomio completo a aquel que tiene, en toda su estructura todos los términos, esto quiere decir que posee términos independientes y hasta un término de mayor grado. Ejemplo de polinomio completo: P(X) = 3x⁴+ 4x³ + 6x – 4.
• Polinomio Incompleto: Es aquel polinomio en el que se puede apreciar que no tiene todos los términos, ya sea desde el independiente hasta el de grado mayor. Ejemplo de polinomio incompleto: P(X) = 3x⁴+ 6x – 4.
• Polinomio Ordenado: Este polinomio se resalta por ser, tal como su nombre lo indica, muy ordenado ya que se aprecia que los monomios que lo conforman se presentan de mayor a menor. Ejemplo: P(X) = 3x⁴+ 6x – 4..
• Polinomios Iguales: Implica que los dos polinomios tienen el mismo grado o bien que los coeficientes de sus términos coinciden. Ejemplo: P(X) = 3x⁴ – 6x – 4. Q(X) = 6x – 4 + 3x⁴.
• Polinomios Semejantes: Esta clasificación refiere al caso en que se considera que dos polinomios pueden ser semejantes si sus partes literales son iguales. Ejemplo: P(X) = 3x⁴ + 6x – 3. Q(X) = 4x⁴ + 8x – 3.

Suma de polinomios

Para realizar la suma de polinomios debemos sumar los coeficientes de aquellos términos que tengan el mismo grado. Para esto, primero se deberán ordenar los polinomios si es que no se encuentran ordenados. Luego se agrupan los monomios del mismo grado, y por ultimo debemos sumar los monomios semejantes.

Veamos un ejemplo:

Tenemos que sumar la siguiente expresión P(x) = 2x³ + 5x − 3,      Q(x) = 4x − 3x² + 2x³.

El primer paso a realizar será ordenar los polinomios:

P(x) = 2x³ + 5x − 3

Q(x) = 2x³ − 3x² + 4x

Luego agruparemos los monomios que tengan el mismo grado:

P(x) + Q(x) = (2x³ + 5x − 3) + (2x³ − 3x² + 4x)

P(x) + Q(x) = (2x³ + 2x³) + (− 3 x²) + (5x + 4x) + (− 3)

Por ultimo sumamos los monomios que son semejantes:

P(x) + Q(x) = 4x³ − 3x² + 9x − 3

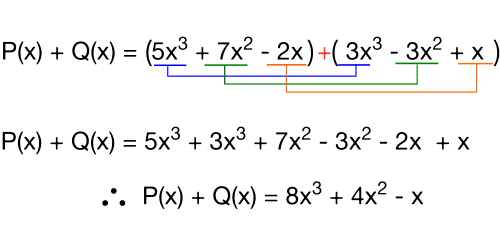
Resta de polinomios

Cuando tenemos casos para resolver de resta de polinomios, debemos sumar el opuesto del sustrayendo. Ejemplo:  P(x) − Q(x) = (2x³ + 5x − 3) − (2x³ − 3x² + 4x)

Primero debemos obtener el opuesto del sustrayendo Qx:

P(x) − Q(x) = 2x³ + 5x − 3 − 2x³ + 3x² − 4x

Luego realizamos la agrupación:

P(x) − Q(x) = 2x³ − 2x³ + 3x² + 5x − 4x − 3

Por ultimo obtendremos el resultado:

P(x) − Q(x) = 3x² + x – 3

Producto de un número por un polinomio

Un producto de un número por un polinomio da como resultado otro polinomio que tiene de grado el mismo del polinomio y como coeficientes la multiplicación de los coeficientes del polinomio por el número. Detallamos un ejemplo:

Producto de un monomio por un polinomio

En este caso se multiplica el monomio por todos y cada uno de los monomios que forman el polinomio. Veamos un ejemplo:

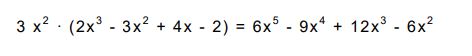
Producto de polinomios

Para poder resolver un producto de polinomios debemos multiplicar cada monomio del polinomio por todos los elementos que componen el segundo polinomio. Luego sumaremos los monomios del mismo grado.

Como resultado de esta operación obtendremos otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.

Simplificación de expresiones algebraicas

Simplificar expresiones algebraicas consiste en escribirla de la forma más sencilla posible. Para poder realizar esta simplificación es necesario conocer las operaciones matemáticas básicas (suma, resta, multiplicación y división), conceptos de expresiones algebraicas tales como variables, coeficientes, potencias y paréntesis, operaciones con potencias y fundamentalmente el orden de las operaciones.

Conceptos a tener en cuenta:

-Suma y resta de variables: Sólo se podrán  sumar o restar variables iguales, es decir, aquellas representadas con la misma letra. Para esto, debemos sumar o restar sus coeficientes y mantener la variable.

-Multiplicación y división de variables: En el caso de estas operaciones, se podrán  multiplicar o dividir variables diferentes o que estén representadas con distintas letras. Para hacerlo, hay que multiplicar o dividir sus coeficientes y mantén las variables.

-Propiedad distributiva: La propiedad distributiva determina que un coeficiente multiplica a cada uno de los términos dentro de un paréntesis.