Actualizado 5 mayo, 2021
Hablamos de divisibilidad cuando tomamos un número, en este caso llamado A, lo dividimos por el número B y nos da como resto cero (En dicho caso decimos que A es divisible por B). A continuación les enseñaremos la divisibilidad del número 6 y les dejaremos una gran cantidad de ejemplos para que puedan entender su funcionamiento.
Criterios de divisibilidad del número 6
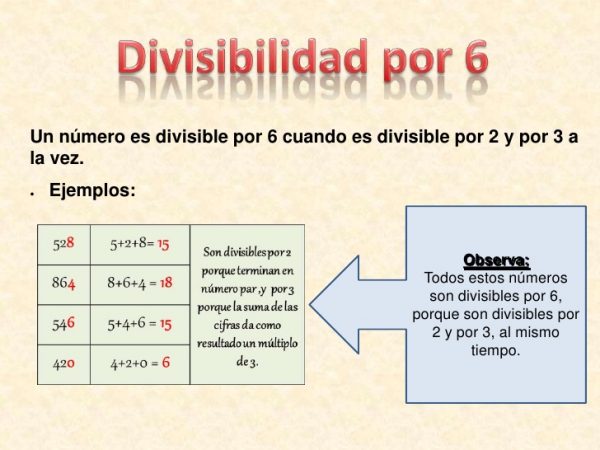
Un número natural es divisible por 6 si y solo si es divisible por 2 y por 3. Por lo tanto, para determinar si un número natural es divisible por 6 es necesario conocer la «regla de la divisibilidad por 2» y la «regla de la divisibilidad por 3».
- Un número natural es divisible por 2 si y solo si el último dígito es par (divisible por 2). Un número natural es divisible por 2 si y solo si el último dígito del número es 0, 2, 4, 6 u 8.
- Un número natural es divisible por 3 si y solo si la suma de sus dígitos es divisible por 3.
Ejemplos prácticos sobre la divisibilidad del 6
Ejemplo número uno: 918
El número natural 918 termina en un número par (8). Como resultado, 918 es divisible por 2 [918 ÷ 2 = 459, resto 0].
La suma de los dígitos del número 918 es 18 (9 + 1 + 8 = 18). Tenga en cuenta que la suma de los dígitos del número 18 es 9 (1 + 8 = 9). Como 18 y 9 son divisibles entre 3, 918 es divisible por 3 [918 ÷ 3 = 306, resto 0].
Dado que 918 es divisible por 2 Y 3, 918 es divisible por 6.
Ejemplo número dos: 916
El número natural 916 termina en un número par (6). Como resultado, 916 es divisible por 2 [916 ÷ 2 = 458, resto 0].
La suma de los dígitos del número 916 es 16 (9 + 1 + 6 = 16). Tenga en cuenta que la suma de los dígitos del número 16 es 7 (1 + 6 = 7). Dado que ni 16 ni 7 son divisibles entre 3, 916 NO es divisible entre 3 [916 ÷ 3 = 305, resto 1].
Aunque 916 es divisible por 2, NO es divisible por 3. Dado que 916 NO es divisible por AMBOS 2 y 3, NO es divisible por 6.
Ejemplo número tres: 915
El número natural 915 termina en un número impar (5). Como resultado, 915 NO es divisible por 2 [915 ÷ 2 = 457, resto 1].
La suma de los dígitos del número 915 es 15 (9 + 1 + 5 = 15). Tenga en cuenta que la suma de los dígitos del número 15 es 6 (1 + 5 = 6). Como 15 y 6 son divisibles entre 3, 915 es divisible por 3 [915 ÷ 3 = 305, resto 0].
Aunque 915 es divisible por 3, NO es divisible por 2. Dado que 916 NO es divisible por AMBOS 2 y 3, NO es divisible por 6.
Ejemplo número cuatro: 913
El número natural 913 termina en un número impar (5). Como resultado, 913 NO es divisible por 2 [913 ÷ 2 = 456, resto 1].
La suma de los dígitos del número 913 es 13 (9 + 1 + 3 = 13). Tenga en cuenta que la suma de los dígitos del número 13 es 4 (1 + 3 = 4). Dado que ni 13 ni 4 son divisibles entre 3, 913 NO es divisible por 3 [913 ÷ 3 = 304, resto 1].
Dado que 913 NO es divisible por 2 o 3, NO es divisible por 6.
Ejemplo número cinco: 716.123.456.789.098.765.432.104
716 123 456 789 098 765 432 104 es divisible por 2 ya que el último dígito es par (divisible por 2).
716123456789098765432104 es divisible por 3 ya que 108 y 9 son divisibles por 3.
NOTA: 7 + 1 + 6 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + 4 = 108
NOTA: 1 + 0 + 8 = 9
Dado que 716123456789098765432104 es divisible por 2 Y 3, también es divisible por 6.
Ejemplo número seis: 716.123.456.789.098.765.432.107
716 123 456 789 098 765 432 107 NO es divisible por 2 ya que el último dígito es impar (NO divisible por 2).
716123456789098765432107 es divisible por 3 ya que 111 y 3 son divisibles por 3.
NOTA: 7 + 1 + 6 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + 7 = 111
NOTA: 1 + 1 + 1 = 3
Aunque 716 123 456 789 098 765 432 107 es divisible por 2, NO es divisible por 3. Dado que NO es divisible por AMBOS 2 y 3, NO es divisible por 6.
Ejemplo número siete: 717.123.456.789.098.765.432.108
El número natural 717 123 456 789 098 765 432 108 termina en un número par (8). Como resultado, es divisible por 2.
La suma de los dígitos del número 717 123 456 789 098 765 432 108 es 113. Tenga en cuenta que la suma de los dígitos del número 113 es 5. Dado que ni 113 ni 5 son divisibles por 3, 717 123 456 789 098 765 432 108 NO es divisible por 3.
NOTA: 7 + 1 + 7 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 0 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0 + 8 = 113
NOTA: 1 + 1 + 3 = 5
Aunque 717 123 456 789 098 765 432 108 es divisible por 2, NO es divisible por 3. Dado que 717 123 456 789 098 765 432 108 NO es divisible por AMBOS 2 y 3, NO es divisible por 6.
Ejemplo número ocho: 717.123.456.789.098.765.432.105
El número natural 717 123 456 789 098 765 432 105 termina en un número impar (5). Como resultado, NO es divisible por 2.
La suma de los dígitos del número 717 123 456 789 098 765 432 105 es 110. Tenga en cuenta que la suma de los dígitos del número 110 es 2. Dado que ni 110 ni 2 son divisibles por 3, 717 123 456 789 098 765 432 105 NO es divisible por 3.
Dado que 717123456789098765432105 NO es divisible por 2 ni por 3, NO es divisible por 6.
Ejemplo número nueve: 42
[Conocemos las reglas de divisibilidad por 2, si el lugar de la unidad del número es 0 o múltiplo de 2, es divisible por 2].42 es divisible por 2. Dado que el ultimo numero es par, es divisible por 2.
[Un número es divisible por 3, si la suma de sus dígitos es múltiplo de 3 o divisible por 3].42 es divisible por 3. Dado que la suma de los dígitos de 42 = 4 + 2 = 6 que es divisible por 3.
42 es divisible por 2 y 3. Por lo tanto, es divisible por 6.
Ejemplo número diez: 144
[Conocemos las reglas de divisibilidad por 2, si el lugar de la unidad del número es 0 o múltiplo de 2, es divisible por 2].144 es divisible por 2. Dado que la unidad de lugar es 4, que es divisible por 2.
[Un número es divisible por 3, si la suma de sus dígitos es múltiplo de 3 o divisible por 3].144 es divisible por 3. Dado que la suma de los dígitos de 144 = 1 + 4 + 4 = 9 que es divisible por 3.
144 es divisible por 2 y 3. Por lo tanto, es divisible por 6.
Ejemplo número once: 180
[Conocemos las reglas de divisibilidad por 2, si el lugar de la unidad del número es 0 o múltiplo de 2, es divisible por 2].180 es divisible por 2. Dado que el lugar de la unidad es 0, es divisible por 2. [Un número es divisible por 3, si la suma de sus dígitos es un múltiplo de 3 o es divisible por 3].
180 es divisible por 3. Dado que la suma de los dígitos de 180 = 1 + 8 + 0 = 9 que es divisible por 3.
180 es divisible por 2 y 3. Por lo tanto, es divisible por 6.
Ejemplo número doce: 258
[Conocemos las reglas de divisibilidad por 2, si el lugar de la unidad del número es 0 o múltiplo de 2, es divisible por 2].258 es divisible por 2. Dado que el lugar de la unidad es 8, que es divisible por 2.
[Un número es divisible por 3, si la suma de sus dígitos es múltiplo de 3 o divisible por 3].258 es divisible por 3. Dado que la suma de los dígitos de 258 = 2 + 5 + 8 = 15 que es divisible por 3.
258 es divisible por 2 y 3. Por lo tanto, es divisible por 6.
Ejemplo número trece: 156
[Conocemos las reglas de divisibilidad por 2, si el lugar de la unidad del número es 0 o múltiplo de 2, es divisible por 2].156 es divisible por 2. Dado que el lugar de la unidad es 6, que es divisible por 2.
[Un número es divisible por 3, si la suma de sus dígitos es múltiplo de 3 o divisible por 3].156 es divisible por 3. Dado que la suma de los dígitos de 156 = 1 + 5 + 6 = 12 que es divisible por 3.
156 es divisible por 2 y 3. Por lo tanto, es divisible por 6.
Ejemplo número catorce: 70
[Conocemos las reglas de divisibilidad por 2, si el lugar de la unidad del número es 0 o múltiplo de 2, es divisible por 2].70 es divisible por 2. Dado que el lugar de la unidad es 0, que es divisible por 2.
[Un número es divisible por 3, si la suma de sus dígitos es múltiplo de 3 o divisible por 3].70 no es divisible por 3. Dado que la suma de los dígitos de 70 = 7 + 0 = 7 que no es divisible por 3.
70 es divisible por 2 pero no por 3. Por tanto, 70 no es divisible por 6.