Actualizado 4 enero, 2021
Sabemos cómo encontrar los divisores de un número dado si dividimos por diferentes números candidatos. Sin embargo, existen algunas reglas sencillas que nos permiten, a primera vista, deducir algunos divisores de los números elegidos. Hoy en este blog te queremos contar información sobre los criterios de divisibilidad del numero 2, del numero 4 y del numero 7 para que puedas aprender un poco mas sobre matemáticas y puedas compartir esta información con quien quieras. Así que disfruta de este blog tan genial y agrega conocimientos sobre matemáticas a tu mente.

¿Qué significa cuando decimos que un número se puede dividir entre otro?
Esto ocurre cuando se hace la división y su resultado es un número entero y el resto es cero. Por ejemplo, el número 12 se puede dividir por 3 porque el resultado es 4 y el resto es cero. Sin embargo, 12 no se puede dividir entre 5, ya que el resto no es 0. Según el lenguaje matemático: “Si D y d son números enteros, se dice que D (dividendo) se puede dividir por d (divisor) si hay un número natural q (cociente) de modo que dxq = D. ”
¿Qué son los criterios de divisibilidad?
Una regla de divisibilidad es una heurística para determinar si un número entero positivo se puede dividir uniformemente por otro (es decir, que no queda resto). Por ejemplo, determinar si un número es par es tan simple como verificar si su último dígito es 2, 4, 6, 8 o 0. Varias reglas de divisibilidad aplicadas al mismo número de esta manera pueden ayudar a determinar rápidamente su factorización prima sin tener que adivinar sus factores primos.
Los criterios de divisibilidad son pautas que nos permiten saber de una manera rápida si un número es divisible entre otro. Es decir, nos permiten saber si cuando los dividamos el resto de la división será cero o no. Los criterios de divisibilidad son muy útiles porque nos ayudan a encontrar con facilidad los divisores de un número determinado. También nos sirven especialmente cuando tenemos que descomponer números en factores primos o saber si un número es primo o compuesto, y por ultimo nos dan pistas cuando tenemos que simplificar fracciones, entre muchas otras cosas mas.
Criterios de divisibilidad del 2
Un número es divisible por 2 si termina con un número par. Cada número cuyo dígito unitario sea 0,2,4,6 u 8 se puede dividir por 2 y esto significa que el número es par.
Por ejemplo:
456 (termina en 6) se puede dividir por 2.
357 (termina en 7) no se puede dividir entre 2.
280 (termina en 0) se puede dividir por 2.
91 (termina en 1) no se puede dividir entre 2.
234 (termina en 4) se puede dividir por 2.
2758 (termina en 8) se puede dividir por 2.
47 (termina en 7) no es divisible entre 2, porque termina en 7, que no es par .
55 (termina en 5) no es divisible entre dos porque termina en 5 que no es un numero par.
67 (termina en 7) no es divisible entre 2, porque termina en 7 que no es un numero par .
89 (termina en 9) no es divisible entre 2, porque termina en 9 que no es un numero par .
88 (termina en 8) se puede dividir por 2 porque termina en numero par.
1234 (termina en 4) se puede dividir por 2 porque termina en numero par.
2444 (termina en 4) se puede dividir por 2 porque termina en numero par.
5545 (termina en 5) no se puede dividir por 2 porque termina en numero 5 que no es un numero par.
7890 (termina en 0) se puede dividir entre 2 porque termina en 0.
826 (termina en 6) si se puede dividir entre 2 porque termina en numero par.
2045 (termina en 5) no se puede dividir en 2 porque no termina en numero par.
Criterios de divisibilidad del 4
Un número es divisible por 4 cuando los dos últimos números son divisibles por 4. A continuación te vamos a mostrar un ejemplo que te ayudara a comprenderlo mejor.
Queremos saber si 448 es divisible por 4, por lo que necesitamos ver si sus dos últimos números, 48, son divisibles entre 4.
48/4 = 12 y el resto es 0. Por lo tanto, 448 es divisible por 4.
Te damos mas ejemplos para que puedas practicar y comprender mejor este criterio:
1020 (20 se puede dividir entre 4) se puede dividir entre 4
721 (21 no se puede dividir entre 4) no se puede dividir entre 4
639 (39 no se puede dividir entre 4) no se puede dividir entre 4
836 (36 se puede dividir entre 4) se puede dividir entre 4.
8100 (00 se puede dividir en 4) es divisible entre 4, porque termina en 00.
23824 es divisible entre 4, porque termina en 24, que es múltiplo de 4 (24=4·6).
632 es divisible entre 4, porque termina en 32, que es múltiplo de 4 (32=4·8)
3615 no es divisible entre 4, porque termina en 15, que no es múltiplo de 4.
4464 (64 es divisible entre 4) porque sus dos últimos números se pueden dividir en 4.
5234 (34 no es divisible entre 4) por lo tanto este numero no se puede dividir entre 4.
1308 (08 es divisible entre 4) por lo tanto este numero se puede dividir entre 4.
7894 (94 no es divisible entre 4) por lo tanto este numero no es divisible entre 4.
Aunque no es habitual verlo, otro criterio de divisibilidad que se puede aplicar también es el siguiente:
Un número es divisible entre 4 si el resultado de sumar el doble del penúltimo dígito y el último da un número múltiplo de 4.
Por ejemplo:
23824 es divisible entre 4, porque 2·2+4=8, y 8 es múltiplo de 4.
632 es divisible entre 4, porque 2·3+2=8, y 8 es múltiplo de 4.
3615 no es divisible entre 4, porque 2·1+5=7, que no es múltiplo de 4.
Criterios de divisibilidad del 7
Ésta es una de las situaciones más difíciles. Tenemos que separar el número de su último dígito. Si el primer conjunto de dígitos separados menos el doble del último dígito es un múltiplo de siete, el número original se puede dividir por 7.
Para que lo entiendas mejor te damos un ejemplo:
¿8274 es divisible por 7?
Vamos a separar la cifra de las unidades:
827 y 4
Al número sin la cifra de las unidades le vamos a restar el doble de las unidades:
827 – 2 x 4=
827 – 8 =
819
Como el número sigue siendo muy grande se debe repetir el mismo procedimiento que hicimos anteriormente:
Separamos la cifra de las unidades:
81 y 9
81 – 2 x 9 =
81 – 18 =
63
Hemos llegado a 63, que es divisible por 7. Por lo tanto, 8274 sí es divisible entre 7.
Te damos unos ejemplos mas para que puedas visualizar el criterio de visibilidad del numero 7:
624 (62-4×2 = 54) (54 no se puede dividir entre 7) no se puede dividir entre 7
525 (52-5×2 = 42) (42 se puede dividir entre 7) se puede dividir entre 7
429 (42-9×2 = 24) (24 no se puede dividir entre 7) no se puede dividir entre 7
707 (70-7×2 = 56) (56 se puede dividir entre 7) se puede dividir entre 7.
119 (11-2×9 = -7) (-7 es múltiplo de 7) se puede dividir entre 7.
546 (54-2×6 = 42) (42 es múltiplo de 7) se puede dividir entre 7.
642 (64-2×2 = 60) (60 no es múltiplo de 7) no se puede dividir entre 7.
345 (34-2×5= 24 ) (24 no es múltiplo de 7) no se puede dividir entre 7.
237 (23-2×7= 9) (9 no es múltiplo de 7) no se puede dividir entre 7.
466 (46-2×6= 34) (34 no es múltiplo de 7) no se puede dividir entre 7.
742 (74-2×2= 70) (70 es múltiplo de 7) se puede dividir entre 7.
Imágenes con ejemplos de criterios de divisibilidad del 2, del 4 y del 7
Hasta aquí te contamos que son los criterios de divisibilidad y cuales son los criterios de divisibilidad del 7, del 4 y del 2. Ahora te vamos a mostrar ejemplos y ejercicios para que puedas poner en practica todo lo que te contamos en este blog tan genial. Así que sigue mirando estas imágenes que te regalamos a continuación y practica todo lo aprendido hasta el momento.

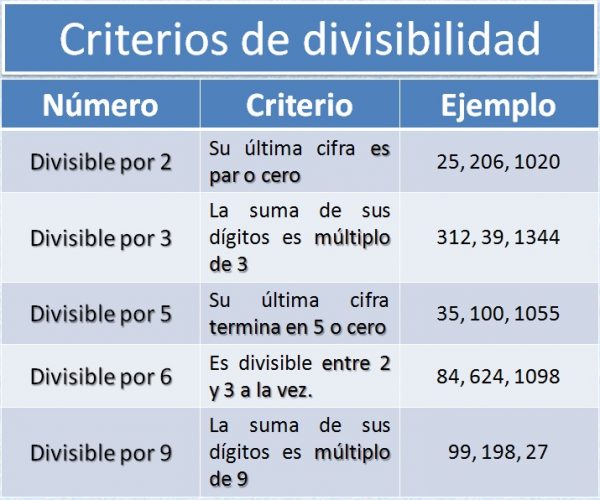
Imagen con cuadro con criterio de divisibilidad del 2.

Imagen con criterio de divisibilidad del numero 7.

Imagen con criterio de divisibilidad del numero 4.



Espero que te haya gustado toda la información que te regalamos aquí sobre los criterios de divisibilidad del numero 2, 4 y 7…