Actualizado 13 abril, 2021
A los estudiantes se les enseña las fracciones a una edad muy temprana, y es uno de los conceptos básicos de Matemáticas que deben comprender para poder resolver varios temas más avanzados que se les irán presentando. Por lo tanto, es importante que entiendan claramente qué son las fracciones y cuáles son los diferentes tipos existentes. Hay principalmente tres tipos de fracciones: fracciones propias, fracciones impropias y fracciones mixtas.
Una fracción se define como una parte, cantidad o proporción pequeña o minúscula de algo. Tiene numerador y denominador. Según el tipo de numerador y denominador, las fracciones son de diferentes tipos. Siga leyendo para obtener más información acerca de ellas.
Qué son las fracciones
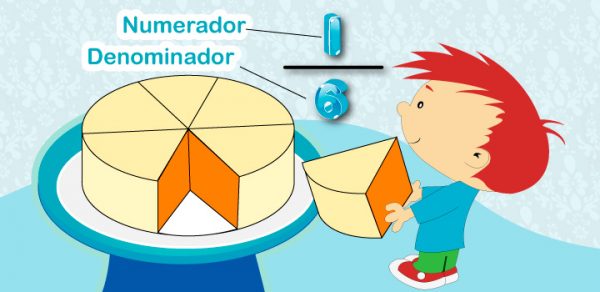
Primero entendamos qué son las fracciones. El término «fracción» representa una cantidad numérica que forma parte de un objeto completo. Podemos entender las fracciones con un ejemplo: Supongamos que tenemos un pastel grande y lo cortamos en 8 porciones iguales. Entonces, cada rebanada es solo 1/8 de la cantidad total de la torta. Por lo tanto, 1/8 es una fracción.
La parte superior de la fracción se llama numerador y la parte inferior es denominador. En este ejemplo, 1 es el numerador y 8 es el denominador. No siempre tratamos con objetos completos en nuestra vida diaria. A veces, tenemos que tratar con partes o porciones de objetos completos. Para cuantificarlos, necesitamos fracciones.
Partes de una fracción
Una fracción tiene tres partes:
- Numerador: la mitad superior de una fracción que representa la cantidad de partes que tiene. En el ejemplo anterior, 1 es el numerador.
- Denominador: La mitad inferior de una fracción que representa el número en el que se divide todo el objeto. En el ejemplo anterior, 8 es el denominador.
- Línea: La línea que divide el numerador y el denominador.
La fracción completa, se lee como «un octavo». Asimismo, ¼ se lee como «un cuarto» y ¾ se lee como «tres cuartos».
Tipos de fracciones con ejemplo
Ahora que sabemos qué son las fracciones y cuáles son las diferentes partes de ellas, veamos cuántos tipos de fracciones hay. Con base en los numeradores y denominadores, las fracciones se clasifican en los siguientes tipos:
1. Fracciones propias
Definición de fracción propia: cuando Numerador < Denominador, es decir, cuando el numerador de una fracción es menor que el denominador, la fracción se denomina fracción propia.
2. Fracciones impropias
Definición de fracción impropia: cuando Numerador > Denominador, es decir, cuando el numerador es mayor que el denominador, la fracción se llama fracción impropia. Tenga en cuenta que puede representar cualquier número natural como una fracción impropia ya que el denominador siempre es 1. Además, todas las fracciones impropias son iguales o mayores que 1.
3. Fracciones mixtas
Definición de fracción mixta: Una fracción que comprende un número natural y una fracción se denomina fracción mixta. Puede convertir una fracción mixta en una fracción impropia y viceversa. Una fracción mixta siempre es mayor que 1.
4. Fracciones similares
Definición de fracción similar: las fracciones que tienen los mismos denominadores son fracciones similares. Por ejemplo, las fracciones 2/7, 3/7, 5/7 y 6/7 tienen el mismo denominador: 7. Por lo tanto, son fracciones similares. La simplificación de fracciones similares es fácil. Por ejemplo, si desea sumar las cuatro fracciones anteriores, todo lo que tiene que hacer es sumar los numeradores. El denominador seguirá siendo el mismo. Entonces, (2/7) + (3/7) + (5/7) + (6/7) = (2 + 3 + 5 + 6) / 7 = 16/7.
5. A diferencia de las fracciones
Definición de fracciones diferentes: las fracciones que tienen denominadores diferentes son fracciones diferentes. Por ejemplo, las fracciones 2/3 y 1/4 tienen denominadores diferentes. Las simplificaciones que involucran fracciones diferentes no son tan sencillas como las fracciones similares.
Suma de fracciones diferentes
Por ejemplo, para sumar las dos fracciones diferentes de arriba, primero, tenemos que convertirlas en fracciones similares. Los pasos involucrados son:
- Calcula el MCM de los dos denominadores 3 y 4.
- MCM de 3 y 4 = 12. Este MCM será el denominador de ambas fracciones.
- Calcula el valor equivalente de la primera fracción (2/3). Para ello, divida el MCM calculado en el paso anterior (12) por el denominador de la primera fracción (3). Entonces, 12 ÷ 3 = 4. Ahora, multiplica 4 por el numerador (2) que da 8. Por lo tanto, la primera fracción se convierte en 8/12.
- Asimismo, calcule el valor equivalente de la segunda fracción (1/4). Para hacer esto, divida el MCM calculado en el primer paso (12) por el denominador de la segunda fracción (4). Entonces, 12 ÷ 4 = 3. Ahora, multiplica 3 por el numerador (1) que da 3. Por lo tanto, la segunda fracción se convierte en 3/12. Ahora, ambas fracciones tienen el mismo numerador: 12.
- Ahora, suma las dos fracciones iguales de manera similar a como se muestra en la sección anterior. Entonces, (8/12) + (3/12) = (8 + 3) / 12 = 11/12. Entonces, (2/3) + (1/4) = 11/12.
6. Fracciones equivalentes
Definición de fracción equivalente: Las fracciones que, al simplificarse, dan el mismo valor, se denominan fracciones equivalentes. Por ejemplo, 1/2 y 50/100 son iguales a 0,5. Por tanto, son fracciones equivalentes.
Preguntas frecuentes sobre diferentes tipos de fracciones
Veamos algunas de las preguntas frecuentes relacionadas con las fracciones y sus tipos:
Pregunta 1: ¿Cuáles son los tipos de fracciones?
Respuesta: Existen principalmente 3 tipos de fracciones:
(i) Fracción propia (por ejemplo, 2/5)
(ii) Fracción impropia (por ejemplo, 7/3)
(iii) Fracción mixta (por ejemplo, 3¾)
Aparte de estas, hay algunos otros tipos de fracciones como, como fracción, fracción a diferencia, fracción equivalente, etc.
Pregunta 2: ¿Qué es un ejemplo de fracción?
Respuesta: Un ejemplo de fracción es 3/8. Decimos que 3 se divide igualmente en 8 partes. Aquí, 3 es el numerador y 8 es el denominador.
Pregunta 3: ¿Cuál es la diferencia entre fracciones iguales y distintas?
Respuesta: Las fracciones que tienen los mismos denominadores son como fracciones, mientras que las fracciones que tienen diferentes denominadores son fracciones diferentes. Por ejemplo, 3/8 y 5/8 son fracciones similares, mientras que 1/6 y 2/5 son fracciones diferentes.
Pregunta 4: ¿Puede una fracción mixta ser menor que 1?
Respuesta: No, las fracciones mixtas siempre son mayores que 1.
Pregunta 5: Defina fracciones propias e impropias con ejemplos.
Respuesta: Cuando el numerador de una fracción es menor que el denominador, se llama fracción propia. Por ejemplo, 3/5. Cuando el numerador de una fracción es mayor que el denominador, se llama fracción impropia. Por ejemplo, 7/3.
Cómo convertir fracción impropia en fracción mixta
Para convertir una fracción impropia en una fracción mixta, el numerador se divide por el denominador y el cociente se escribe como un número entero y el resto como el numerador.
Ejemplo: Convierta 17/4 en una fracción mixta.
Para solucionar este problema, estos son los pasos a seguir
- Divida el numerador por el denominador.
- El cociente es 4 y el resto es 1.
- Combinar el número entero 4 con la fracción 1/4
- 4 1/4 es la fracción mixta.
Ejemplo 2: Convierta 14/9 en una fracción mixta.
- Empiece por dividir el numerador por el denominador.
- 14/9 = 1 y 5 como resto.
- Tome 1 como el número entero y 5 como el numerador,
- Escriba la fracción como: 14/9 = 1 5/9
- Nota: Si durante la división no hay resto, tome el cociente como un número entero.
Cómo convertir fracciones mixtas como una fracción propia
Una fracción mixta se puede expresar como una fracción propia. Esto lo hice multiplicando el denominador de la fracción por el número entero y el producto sumado al numerador. Por ejemplo, para convertir una fracción mixta 2 1/3 en una fracción impropia, se siguen los siguientes pasos:
- Multiplica el denominador por el número entero.
- Para este caso, 2 es el número entero y 3 es el denominador. 2 x 3 = 6
- Agregue el producto al numerador. 6 + 1 = 7
- Ahora el numerador cambia a 7 y el denominador sigue siendo 3.
- Escriba el resultado como una fracción impropia 7/3.
Tomemos otro ejemplo, supongamos que queremos convertir 52/3 en una fracción impropia.
- En primer lugar, multiplique el denominador por el número entero y sume este producto al numerador. 3 x 5 = 15
- Agregue el numerador al producto. 15 + 2 = 17
- Escriba la fracción tomando 17 como el nuevo numerador y quedando 5 como denominador.
- El resultado es 17/5