Actualizado 23 julio, 2020
Convivimos a diario con figuras geométricas y no somos consientes de ello. Desde los cuadros que tenemos colgados en nuestro hogar, hasta el televisor o la taza con la que desayunamos todas las mañanas. Todos nuestros artículos de uso cotidianos están compuestos por figuras geométricas. El día de hoy les enseñaremos los principales tipos existentes, seguido de una explicación detallada para poder calcular su area y volumen.
¿Qué son las figuras geométricas?
Las figuras geométricas se pueden definir como formas o áreas cerradas constituidas por un límite que se crea combinando cantidades específicas de curvas, puntos y líneas. Los triángulos, círculos, trapecios, cuadrados, rectángulos, cubos, corazones, diamantes, etc. son algunas de las figuras geométricas más populares. Otros, como los polígonos, se han descrito en función de su número de lados.
Hay muchas formas bidimensionales y tridimensionales en geometría. Cosas como marcos de fotos, conos de helados, bolas, bloques, ladrillos, etc. reflejan ejemplos en la vida diaria. Las formas no son más que figuras geométricas simples que tienen un límite específico y una área de superficie interior y exterior.
Algunas figuras son 2-D y otras 3-D. Para dibujar cualquiera de estas, uno comienza con una línea, un segmento de línea o una curva. Dependiendo del número y la disposición de estas líneas, obtenemos diferentes tipos de formas y figuras como un triángulo (que consiste en una figura donde se conectan tres segmentos de línea), un Pentágono (segmentos de cinco líneas), etc.
Tipos de figuras geométricas
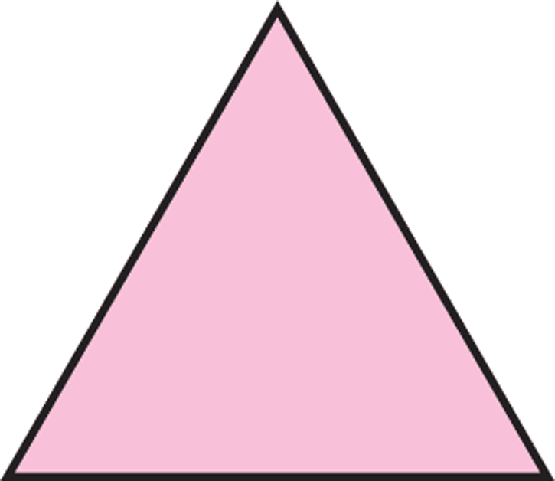
Triángulo
Triángulo es un polígono, que está formado por tres lados y consta de tres aristas, tres vértices y, además, la suma de sus ángulos internos es igual a 180 grados.
- Equilátero: Todos los lados tienen la misma longitud y todos los ángulos son iguales.
- Isósceles: Dos lados tienen la misma longitud y dos ángulos son del mismo tamaño.
- Escaleno: Todos los lados son de diferentes longitudes y todos los ángulos son de diferentes tamaños.
- Ángulo agudo: Un triángulo con tres ángulos agudos, cada uno inferior a 90 °.
- Ángulo recto: Un triángulo que contiene un ángulo recto (90 °).
- Ángulo obtuso: Un triángulo que contiene un ángulo obtuso (más de 90 °)
Circulo
Se le llama circulo a la figura geométrica donde cada punto de la superficie es equidistante al centro de la misma.
Cuadrado
El cuadrado es un cuadrilátero donde los cuatro lados y ángulos (90 °) son iguales.
Rectángulo
Un cuadrilátero que tiene sus lados opuestos de igual longitud y ángulos interiores rectos.
Paralelogramo
Un paralelogramo es un cuadrilátero con dos pares de lados paralelos y ángulos opuestos de igual medida.
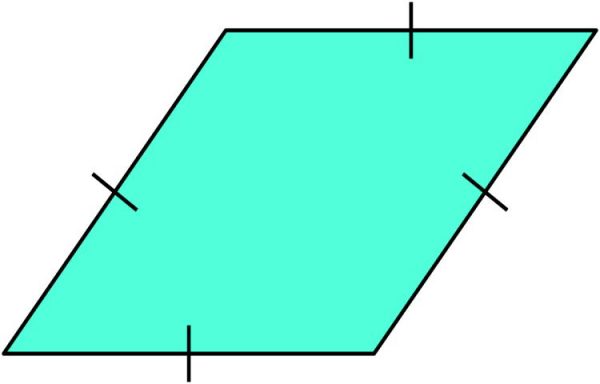
Rombo
Todos los lados tienen la misma longitud, pero ninguno de los ángulos son ángulos rectos.
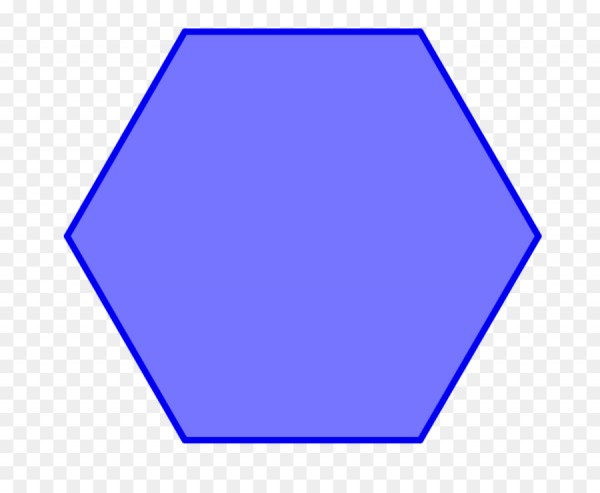
Polígonos
Estos están formados por segmentos de líneas y no poseen curvas. Son estructuras cerradas basadas en diferentes longitudes de lados y diferentes ángulos.
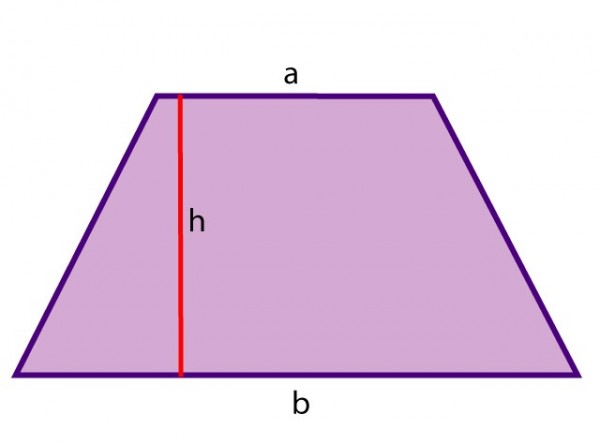
Trapecio
Un par de los lados opuestos son paralelos.
Ejercicios con figuras geométricas
Ejercicios para practicar las figuras geométricas
Ejercicios para aprender las figuras geométricas
Ejercicios para que los niños puedan aprender las figuras geométricas
Ejercicios con figuras geométricas para niños
Ejercicios para enseñar las figuras geométricas a los niños
Ejercicios fáciles para enseñar las figuras geométricas
Ejercicios de geometría para niños
¿Cómo calcular el área de figuras geométricas 2d?
Área del triángulo
- Área = ½ × b × h
- b = base
- h = altura vertical
Área del cuadrado
- Área = a^2
- a = longitud del lado
Área del rectángulo
- Área = w × h
- w = ancho
- h = altura
Área del paralelogramo
- Área = b × h
- b = base
- h = altura vertical
Área del trapecio
- Área = ½ (a + b) × h
- h = altura vertical
Área del circulo
- Área = π × r2
- Circunferencia = 2 × π × r
- r = radio
¿Cómo calcular el volumen de figuras geométricas 3d?
Fórmula de área y volumen de una esfera
Una esfera es una figura sólida donde cada punto de la superficie es equidistante del centro de la esfera. Esta distancia es el radio, r, de la esfera.
- Área de superficie = 4πr2
- Volumen = 4⁄3πr3
Fórmula del área y volumen de un prisma
Un prisma es una forma geométrica que consiste en una pila de formas de base idénticas apiladas una encima de la otra hasta una profundidad d. En este caso realizamos una pila de triángulos.
- Área de superficie de un prisma = 2 × (Área de la forma de la base) + (Perímetro de la forma de la base) × (d)
- Volumen de un prisma = (Área de forma de base) × d
Fórmula de área y volumen de una caja
Consiste en una pila de rectángulos de largo L y ancho W apilados uno encima del otro a una profundidad de D.
- Área de superficie de una caja = Suma de las áreas de cada cara de la caja, o
- Área de superficie de una caja = 2 (L × W) + 2 (L × D) + 2 (W × D)
- Volumen de una caja = L × W × D
Fórmula del área y volumen de un cubo
Un cubo es una caja especial donde todos los lados tienen la misma longitud.
- Área de superficie de un cubo = 6a2
- Volumen de un cubo = a3
Fórmula del área y volumen de un cilindro
Un cilindro es un prisma donde la forma de la base es un círculo.
- Área de superficie de un cilindro = 2πr2 + 2πrh
- Volumen de un cilindro = πr2h
Fórmula del área y volumen de una pirámide
Una pirámide es una forma sólida que consiste en una base poligonal y caras triangulares que se encuentran en un punto común sobre la base. La que analizaremos aquí se trata de una pirámide rectangular. Hay dos medidas importantes necesarias para calcular el área de superficie y el volumen de esta. La primera es la altura de la pirámide (h). Esta es la distancia desde la base hasta el punto donde se encuentran las caras triangulares. La segunda es la altura de los triángulos de la cara individual.
Área de superficie de una pirámide = (suma de las áreas de cada cara) + (área de la base)
- Volumen de una pirámide = 1⁄3 A × h
Para pirámides con triángulos idénticos
- Área de superficie de una pirámide = (1⁄2 × Perímetro de forma de base × s) + (Área de forma de base)
- Volumen de una pirámide = 1⁄3 A × h
Si la base de la pirámide es un cuadrado (a = b), entonces
- Área de superficie de una pirámide cuadrada = a2 + √3 (a2)
- Volumen de una pirámide cuadrada = √5 (a3 / 6)
Fórmula del área y volumen de un cono
Un cono es una pirámide con una base circular con radio r y altura h. La longitud lateral s se puede encontrar usando el Teorema de Pitágoras.
- s2 = r2 + h2
- s = √ (r2 + h2)
- Área de superficie de un cono = πr2 + πrs
- Volumen de un cono = 1⁄3 (πr2h)