Actualizado 27 julio, 2021
Un número es divisible por 3 cuando la suma de los valores absolutos de sus cifras es múltiplo de 3. La mejor manera es dividir un número entre 3 y si el resto es igual a cero entonces el número sí es divisible entre 3.
Números divisibles por 3
Por ejemplo, 45 es divisible por 3, porque si lo dividimos por 3 es 15 y el resto de la división es 0, por eso podemos decir que es divisible por 3. El número 3627 también es divisible por 3 porque la suma de los dígitos es 18, que es divisible por 3.

¿Que son los criterios de divisibilidad?
Los criterios de divisibilidad sirven para saber si un determinado número se puede dividir por otro sin que se necesario realizar un cálculo. Cuando decimos que un número se puede dividir por otro, nos referimos a que cuando se hace la división y su resultado es un número entero y el resto es cero. Por ejemplo el número 12 se puede dividir por 3 porque el resultado es 4 y el resto es 0, sin embargo 12 no se puede dividir por 5, ya que el resultado no es 0. Según el lenguaje matemático si A y a son números enteros, se dice q A (dividendo), se puede dividir por a (divisor), si hay un número natural q (cociente) de modo que axq=A.
Criterios de divisibilidad
Los criterios de divisibilidad son formas de saber si un número divide al otro sin realmente llevar a cabo la división. Tal como sabemos, en las ciencias matemáticas existen una gran variedad de operaciones y cada una de ellas posee sus propias reglas y para poder lograr el resultado correcto debemos resolver cada operación siguiendo estos pasos.
Cuando hablamos de divisibilidad de un número, debemos saber que existen determinadas reglas que nos ayudarán a entender y resolver cada operación de una manera más simple. Los criterios de divisibilidad son una herramienta muy útil para lograr simplificar estos problemas con las divisiones.
Cada uno de estos criterios varia según el número que se trate, por lo tanto podemos decir que cada número tiene sus propias reglas de divisibilidad.

Los criterios de divisibilidad nos ayudarán a:
- Encontar con facilidad los divisores de un número.
- Descomponer números en factores primos o bien saber si un número es primo o compuesto.
- Brindarnos pistas sobre cuando tendremos que simplificar fracciones.
- Saber si un número es divisible por otro sin tener que dividirlos.
Reglas de divisibilidad
La divisibilidad de un número es un recurso fundamental al que podremos recurrir cuando necesitemos relizar alguna operación matemática tal como descomponer un número. Para esto es que existen diferentes reglas o criterios que varían según el número con que se está trabajando.
por ello es necesario poder sber cuales son esos criterios para que al momento de tener que resolver un problema, podamos recurrir a dichos conocimientos y así simplificar las operaciones. Las reglas de divisibilidad del número 3 parten del lema de que, un número es divisible entre 3 si la suma de sus cifras es múltiplo de 3.
Ejemplos
- El número 45 es divisible entre 3, ya que la suma 4+5 = 9 y 9 es múltiplo de 3, (9=3×3)
- 35673 es divisible entre 3 ya que 3+5+6+7+3=24 y 24 es múltiplo de 3 (24=3×8)
- 5908 no es divisible entre 3 porque 5+9+0+8=22 y 22 no es múltiplo de 3.
Cuando el número tenga tres cifras, no es necesario sumar dichas cifras ya que son tres. De éste modo como la suma total de las cifras es menor es más simple ver si es o no múltiple de tres.
Podemos decir entonces que un número entero es divisible por 3 si la suma de sus cifras es divisible por tres.
394 no es divisible por 3 ya que si sumamos 3+9+4 nos da como resultado 16 y 16 no es divisible por 3, ya que su resto no es cero. Este método también se puede utilizar para encontrr el resto en la división, es decir se suman las cifras y se divide el resultado por tres, si el resto de esta división es cero, estamos frente a un múltiplo de tres.
Siguiendo el ejemplo anterior, la suma de 394 es 16, si dividimos 16 por 3, nos queda un resto de 1 y así podremos ver que este número no es un múltiplo de 3.
Otra paauta a tener en cuenta sobre este criterio es ante un número con muchas cifras , si el resultado no es múltiplo de tres tampoco lo serán sus simplificaciones.
Por Ejemplo:
Queremos saber si 9783592 es múltiplo de 3, por lo tanto sumanos 9+7+8+3+5+9+2 obtendremos como resultado 43 que no es divisible por 3, ahora si sumamos 4+3 tendremos 7 y tampoco es divisible por 3. Por eso cuando enfrentamos la pregunta si tal númeroes divisible por 3, lo más práctico será dividir ese número entre 3 y analizar su resto y si es igual a 0 entonces sabremos que sí. Pero si el número que tenemos es muy alto no siempre tendremos que dividir por tres ya que hay una manera más simple de calcularla, sumamos las cifras del número y si obtenemos un resultado que es múltiplo de 3 ya sabremos que es divisible por 3, de lo contrario sabremos que no.
Divisibilidad y números primos
En muchos problemas es necesario saber si el reparto de varios elementos en diferentes grupos se puede hacer equitativamente, es decir, si el número de elementos dividido entre el número de grupos sería una división entera con resto o sin resto. Caso de que dividir a un número entero n entre otro número entero d, la división sea exacta sin resto, diremos que n es un múltiplo de d, que n es divisible entre d, que d es divisor de n oque d divide a n. En este caso existe un tercer entero (cociente) c, tal que n=cxd. En general aplicamos la divisibilidad aa números enteros, pudiendo ser positivos o negativos. Por ejemplo, 45 es divisible por 15 y -33 divide a 198, siendo los cocientes respectivos 3 y -6.
Más reglas sobre la divisibilidad
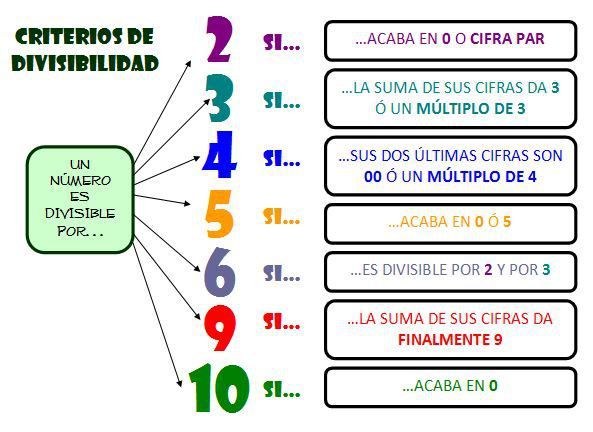
El que el número sea divisible por 2,3,4,5,8,9,10 u 11 es sencillo de comprobar, un número entero cualquiera n:
- Es divisible entre 2 si y sólo si su última cifra es par.
- Es divisible entre 3 si y sólo si la suma de las cifras de n es múltiplo de 3
- Es divisible entre 4 si y sólo si su última cifra es par, pero no múltiplo de 4 y su peniúltima cifra es impar o si su última cifra es múltiplo de 4 y su penúltima cifra es par
- Es divisible entre 5 si y sólo si su última cifra es 0 o 5
- Es divisible entre 8 si y sólo si el número formado por sus tres últimas cifras es múltiplo de 8
- Es divisible entre 9 si y sólo la suma de las cifras de n es múltiplo de 9
- Es divisible entre 10 si y sólo si la última cifra es 0
- Es divisible entre 11 si y sólo si la suma de sus cifras en posición par, menos la suma de sus cifras en posición impar es múltiplo de 11 incluído el 0
Cuando las reglas anteriores no valen
Si nos toca dividir un entero entre los números anteriores, no es complicado preveer si el resultado es cero o no. Pero nos puede tocar dividir un número como 7, 13, 47 o 2010, en el caso de los primeros tres números, poco podemos hacer, salvo realizar la división y ver si da exacto, en el caso de 2010, podemos aplicar el razonamiento de 2010=2x3x5x67 podemos ver que si el número es divisible entre 10 y también es divisible entre 3. Caso de que sí sea divisible ente 3 o 10 hemos acabado, el número no será divisible por 2010.