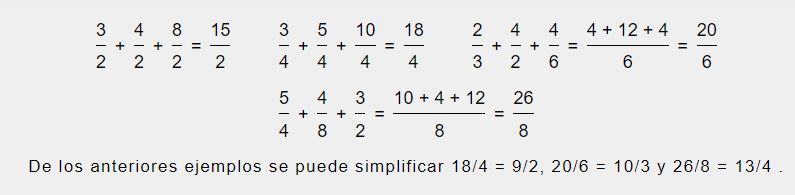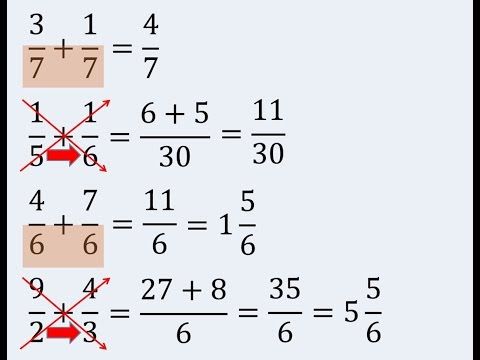Actualizado 24 enero, 2023
Se conoce como fracciones a la representación de las partes de un todo. Al dividir algo en partes iguales y tomamos una determinada cantidad de esta, la forma que tenemos de representarlo es por medio de las fracciones.
Por medio de las fracciones lo que estamos dividiendo es un entero y cada parte es una fracción de dicho entero.
Con las fracciones se pueden hacer las operaciones matemáticas de suma, resta, división y multiplicación. En el día de hoy, conocemos como son las sumas de fracciones y veremos ejemplos y ejercicios.
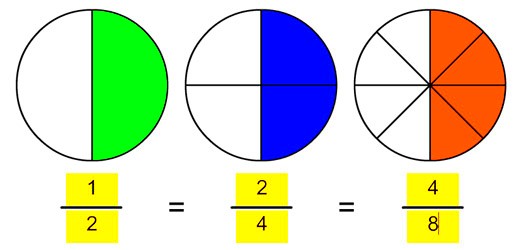
Partes de una fracción
Las fracciones se componen de dos partes, el término superior (que es el número que va arriba) y recibe el nombre de numerador, y el termino inferior (que es el numero que va abajo) y recibe el nombre de denominador.
El numerador representa a las partes que se han tomando de un todo y el denominador representa el total de partes en que se dividió el entero (que es el numerador).
Veamos un ejemplo para entenderlo bien:
Si tenemos una torta a la cual la cortamos en ocho partes iguales, cada porción representa un octavo (1/8) del total. Si comemos tres porciones de nuestra torta, podemos decir que comimos tres octavos (3/8) del total.
En este caso el número ocho representa al denominador y siempre será el mismo.

Tipos de fracciones
Existen diferentes tipos de fracciones. A continuación detallaremos cada una de ellas.
- Fracción propia
Se denomina como fracción propia a aquella en que el numerador es menor que el denominador, esto quiere decir que representa un numero mas chico que un entero. Algunos ejemplos: un sexto (1/6), cuatro octavos (4/8), dos tercios (2/3).
- Fracción impropia
Las fracciones impropias son lo contrario a las fracciones propias. Son aquellas en las que el numerador es mayor que el denominador, esto quiere decir que representa un número mas grande que el entero. Por ejemplo: ocho tercios (8/3), tres medios (3/2), siete medios (7/2).
- Fracciones comunes y decimales
Se conoce como fracciones comunes a aquellas cuyo denominador no es la unidad seguida de ceros. Por ejemplo: dos quintos (2/5), un séptimo (1/7), ocho onceavos (8/11).
Las fracciones decimales, son aquellas cuyo denominador si es la unidad seguida de ceros. Por ejemplo: dos decimos (2/10), una centésima (1/100), veinticinco milésimas (25/1000).
Suma de fracciones
Tal como decíamos anteriormente con las fracciones es posible realizar operaciones matemáticas. A continuación veremos como es la suma de fracciones.
Para poder obtener el resultado de la suma de las fracciones, primero debemos identificar si esta suma posee igual denominador o distinto denominador. Por lo tanto en la suma de fracciones pueden darse dos casos:
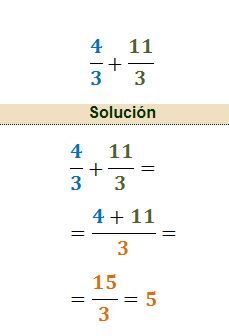
-Que los denominadores sean iguales, en este caso se suman los numeradores y se mantiene el mismo denominador. Por ejemplo:
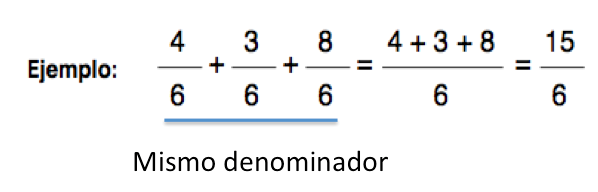
-Que los denominadores sean distintos, en este caso se procederá a transformar las fracciones para lograr que tengan el mismo denominador.
Los procesos para resolver las sumas de estos tipos de fracciones pueden ser por dos métodos distintos:
- El primer método se puede resolver de dos maneras.
- a) Método de la división de los denominadores por los numerados, el cual consiste en buscar el común denominador de las fracciones que queremos sumar. Para lograr esto debemos multiplicar los denominadores de las fracciones.
Veamos un ejemplo:
Supongamos que tenemos una suma de 1/2 + 3/5. En este caso buscamos el múltiplo común de los denominadores 2 y 5, el cual es el numero 10. Luego de obtener este múltiplo vamos a dividirlo por cada uno de los denominadores y a este resultado lo multiplicamos por el numerador de cada uno. De esta manera nos quedaría:
10 dividido 2 = 5. Luego hacemos 5 x 1 = 5
10 dividido 5 = 2. Luego hacemos 2 x 3 = 6
De este modo nos quedara en el denominador nos quedara 10 y en numerador será la suma de 5 + 6. Por lo tanto el resultado de esta suma es 11/10.
- b) Método de la multiplicación de la cruz: Este caso consiste en buscar el común denominador de las fracciones que se van a sumar. Veamos un ejemplo:
Tenemos para sumar las fracciones 1/3 + 3/5. Lo primero que haremos será multiplicar los denominadores para obtener el múltiplo común: 3 x 5 = 15. Luego multiplicamos el numerador de la primera fracción por el denominador de la segunda fracción (por esto se lo llama método de la cruz) y el resultado de esta operación lo ubicamos en el numerador con el signo de la fracción. De este modo nos quedaría 1 x 5 = 5.
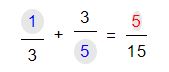
Una vez realizada esta operación continuamos multiplicandos el denominador de la primera fracción por el numerador de la segunda y el resultado se colocará en el numerador con el signo de la fracción. De este modo nos quedaría 3 x 3 = 9.
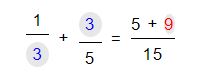
Por ultimo nos quedará sumar los resultados para obtener la resolución de la suma.
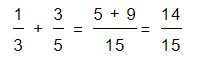
- El segundo método consiste en la obtención del minino común múltiplo de los denominadores, por lo cual una vez identificado este mayor múltiplo entre ellos podremos realizar la suma de las fracciones.
En este caso para poder lograr el mismo denominador debemos utilizar el mínimo común múltiplo (mcm) de los denominadores. Una vez que logramos el número más pequeño que sea múltiplo de los denominadores, se divide al mismo (mcm) por cada denominador, y el resultado debemos multiplicarlo por su correspondiente numerador. Veámoslo en un ejemplo:
Queremos sumar las siguientes fracciones: 1/2 + 4/6. Lo primero que vamos a realizar será buscar el mayor común denominador entre 2 y 6, el cual es 6. Una vez que obtenemos este numero lo dividimos por el denominador de la primer fracción, seis dividido dos (6/2). El resultado de esta división (tres) se multiplica por el numerador de la misma fracción, en este caso sería 3 x 1 = 3.
Este resultado se coloca en el numerador de la resolución con el signo de la fracción. El mismo procedimiento haremos con la otra fracción y su resultado será sumado al numero obtenido anteriormente.
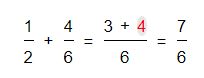
¿Cómo proceder cuando tenemos más de dos fracciones?
En el caso de que tengamos que resolver la suma de más de dos fracciones, el procedimiento es similar a lo detallado anteriormente.
Lo primero que debemos realizar es identificar si tienen igual o diferente denominador. Si los denominadores de las fracciones son iguales sumaremos todos los numeradores y dejamos el denominador común.
Si los denominadores de las fracciones que queremos sumar son distintos, debemos optar por encontrar el mínimo común múltiplo de todos los denominadores y aplicar el método detallado para este tipo de fracciones.
Suma de fracciones mixtas
¿Que son las fracciones mixtas? una fracción mixta es aquella que representa un numero entero y una fracción propia, es decir es la suma de una parte entera más una parte fraccionaria.
Cuando se presentan casos de sumas de fracciones mixtas, es fundamental que la parte entera este expresada como una fracción con el mismo denominador que en la parte fraccionaria que lo acompaña. En el caso que el numero es dado con enteros y decimales, lo primero que habrá que realizar es convertir la parte decimal a fracción.
Veamos un ejemplo, tenemos la siguiente suma de fracción mixta:
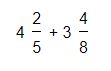
Lo primero que debemos hacer es multiplicar la parte entera por el denominador de la fracción. Esto es:
4 x 5 =20
3 x 8 = 24
El resultado de dicha multiplicación se sumará con el numerador de la fracción:
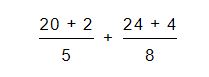
Por último, una vez que convertimos las fracciones mixtas podremos realizar la suma para obtener la respuesta buscada:
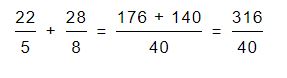
De esta forma podremos resolver suma de fracciones mixtas.
A continuación dejamos algunos ejercicios de suma de fracciones con sus correspondientes respuestas.