Actualizado 26 febrero, 2021
En el día de hoy les traemos una serie de problemas para que puedan practicar la suma, resta, multiplicación y división de fracciones desde la comodidad de su casa. Aquí no solo encontrarán una gran cantidad de ejercicios, sino también una guía súper completa para aquellos que recién están empezando y aún no saben como resolverlos.
Cómo se suman las fracciones
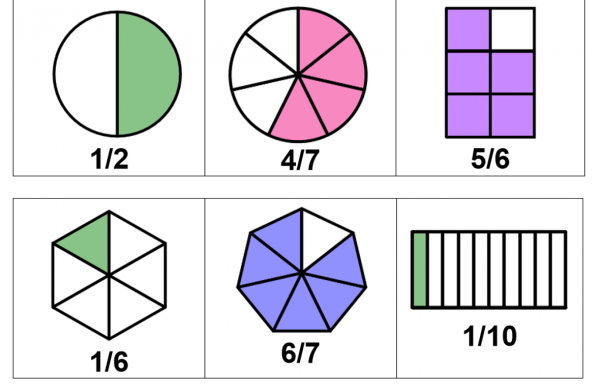
Una fracción como 3/4 dice que tenemos 3 de las 4 partes en las que se divide el todo. El numero 3 es llamado numerador, y el numero 4 denominador.
Para sumar fracciones hay que seguir tres pasos sencillos:
- Paso 1: Asegúrese de que los números inferiores (los denominadores) sean los mismos
- Paso 2: Sume los números superiores (los numeradores) y coloque esa respuesta sobre el denominador
- Paso 3: Simplifique la fracción (si es necesario)
Ejemplo de suma con igual denominador:
1/4 + 1/4
Paso 1. Los números inferiores (los denominadores) ya son los mismos. Vaya directamente al paso 2.
Paso 2. Sume los números superiores y coloque la respuesta sobre el mismo denominador:
1/4 + 1/4 = (1 + 1) / 4 = 2/4
Paso 3. Simplifique la fracción:
2/4 = 1/2
Ejemplo de suma con diferente denominador:
1/3 + 1/6
Paso 1: Los números inferiores (denominador) son diferentes. Necesitamos hacerlos iguales antes de que podamos continuar, porque no podemos restarlos así. El número «6» es dos veces más grande que «3», por lo que para hacer que los números de abajo sean iguales, podemos multiplicar la parte superior e inferior de la primera fracción por 2, así:
(1×2) / (3×2) = 2/6
Importante: multiplique tanto la parte superior como la inferior por la misma cantidad para mantener el valor de la fracción igual. Ahora las fracciones tienen el mismo número de abajo («6»), así que podemos ir al paso 2.
Paso 2: Sume los números superiores y colóqueles sobre el mismo denominador:
2/6 + 1/6 = (2 + 1) / 6 = 3/6
Paso 3: Simplifique la fracción:
3/6 = 1/2
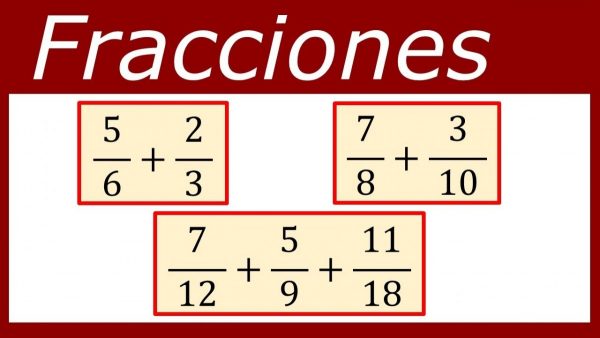
Ejercicios de suma de fracciones
La suma de fracciones se enseña típicamente a partir del 4º grado, con fracciones iguales (mismo denominador, como 3/8 + 2/8). Los niños comienzan usando ejemplos como los que les dejamos con anterioridad, y gráficos (como el de pizza o torta) para entender el concepto y luego comienzan a intentar con problemas abstractos.
Luego, en quinto grado, los estudiantes abordan la suma de fracciones diferentes (fracciones con denominadores diferentes, como 3/4 + 2/5) y números mixtos con partes fraccionarias diferentes. El procedimiento para esto implica convertir las fracciones que se van a sumar en fracciones equivalentes con un denominador común. Después de la conversión, tienes fracciones similares (fracciones con el mismo denominador) que puedes sumar fácilmente.
Ejercicios de suma de fracciones con el mismo denominador
Ejercicios de suma de fracciones con diferente denominador
Cómo se restan las fracciones
Hay 3 sencillos pasos para restar fracciones
- Paso 1: Asegúrate de que los números inferiores (los denominadores) sean los mismos
- Paso 2: Reste los números superiores (los numeradores). Pon la respuesta sobre el mismo denominador.
- Paso 3: Simplifique la fracción (si es necesario).
Ejemplo de resta con igual denominador:
3/4 – 1/4
Paso 1. Los números inferiores ya son los mismos. Vaya directamente al paso 2.
Paso 2. Reste los números superiores y coloque la respuesta sobre el mismo denominador:
3/4 – 1/4 = (3−1) / 4 = 2/4
Paso 3. Simplifique la fracción:
2/4 = 1/2
Ejemplo de resta con diferente denominador:
1/2 – 1/6
Paso 1. Los números de abajo (los denominadores) son diferentes. Necesitamos hacerlos iguales antes de que podamos continuar, porque no podemos restarlos así:
1/2 – 1/6 =?
Para hacer que los números inferiores sean iguales, multiplique la parte superior e inferior de la primera fracción (1/2) por 3 de esta manera:
(1×3) / (2×3) = 3/6
Y ahora nuestra pregunta se ve así:
3/6 – 1/6
Los números inferiores (los denominadores) son los mismos, por lo que podemos ir al paso 2.
Paso 2. Reste los números superiores y coloque la respuesta sobre el mismo denominador:
3/6 – 1/6 = (3−1) / 6 = 2/6
Paso 3. Simplifique la fracción:
2/6 = 1/3
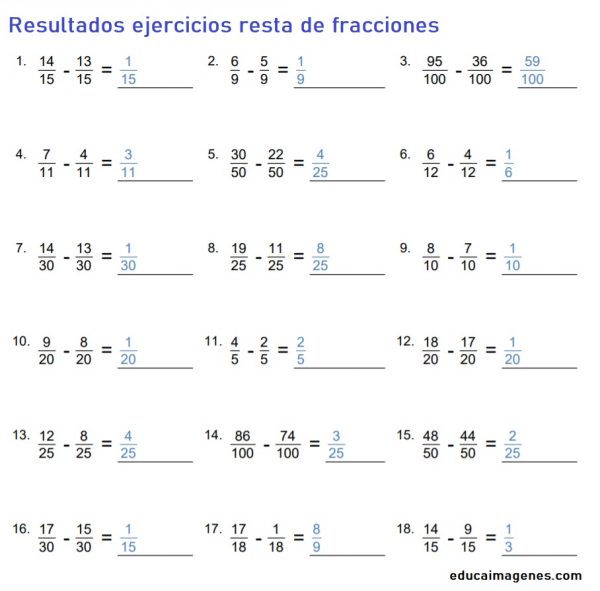
Ejercicios de resta de fracciones
Lo primero que debe saber antes de continuar con los ejercicios de resta es cómo calcular el mínimo común múltiplo de diferentes números. Si la fracción tiene el mismo denominador:
- Escriba el denominador que tienen las fracciones en la fracción final.
- Reste los numeradores y escriba la respuesta en la fracción final.
Si las fracciones tienen diferentes denominadores:
- Encuentre el mínimo común múltiplo de los denominadores de las fracciones.
- Comience a escribir las nuevas fracciones equivalentes con el mínimo común múltiplo como denominador de estas nuevas fracciones.
- La fracción final tendrá el mismo denominador que las otras fracciones.
- Reste los numeradores y escriba las respuestas en la fracción final.
Ejercicios de resta de fracciones con igual denominador
Ejercicios de resta de fracciones con diferente denominador
Cómo se multiplican las fracciones
Multiplique los numeradores, multiplique los denominadores. Hay 3 sencillos pasos para multiplicar fracciones:
- Paso 1: Multiplique los números superiores (los numeradores).
- Paso 2: Multiplique los números de abajo (los denominadores).
- Paso 3: Simplifique la fracción si es necesario.
Ejemplo solo con fracciones:
1/2 × 2/5
Paso 1. Multiplique los números superiores:
1/2 × 2/5 = 1 × 2 = 2
Paso 2. Multiplique los números de abajo:
1/2 × 2/5 = (1 × 2) / (2 × 5) = 2/10
Paso 3. Simplifique la fracción:
2/10 = 1/5
Ejemplo con fracciones y números enteros:
¿Qué hay de multiplicar fracciones y números enteros? Haz que el número entero sea una fracción, poniéndole debajo del mismo un 1 (en su denominador).
5 también es 5/1
Luego continúe como antes. Ejemplo:
2/3 × 5
Convierta 5 en 5/1:
2/3 × 5/1
Ahora sigue adelante con normalidad. Multiplique las partes superiores e inferiores:
2/3 × 5/1 = (2 × 5) / (3 × 1) = 10/3
La fracción ya es tan simple como puede ser.
Respuesta = 10/3
Ejercicios de multiplicación de fracciones
Aprender a multiplicar fracciones, ya sea fracción por fracción o multiplicar fracciones por números enteros, es una habilidad importante que todo estudiante de matemáticas debe aprender en algún momento. Para ello hay una regla fundamental: Siempre que multiplique fracciones, multiplique los numeradores y luego multiplique los denominadores.
Multiplicar fracciones es tan simple como eso, y aplicar la regla a una variedad de problemas diferentes es igual de fácil. Sigamos adelante y apliquemos esta regla en algunos ejercicios.
Ejercicios de multiplicación de fracciones
Ejercicios de multiplicación de fracciones y números enteros
Cómo se dividen las fracciones
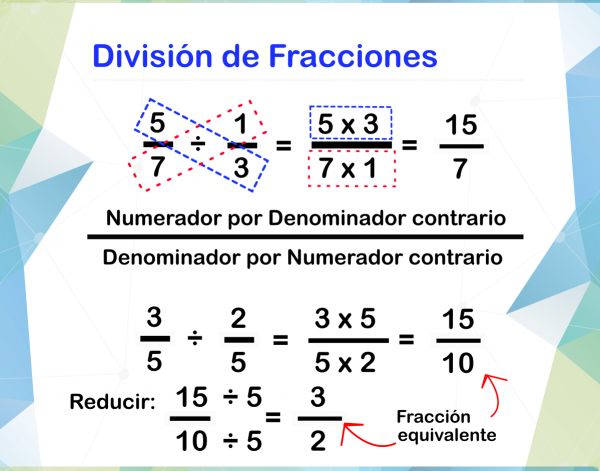
De la vuelta a la segunda fracción y luego multiplique. Hay 3 pasos simples para dividir fracciones:
- Paso 1: Pon la segunda fracción (la que quieres dividir) boca abajo (ahora es recíproca).
- Paso 2: Multiplica la primera fracción por ese recíproco
- Paso 3: Simplifique la fracción (si es necesario)
Ejemplo:
1/2 ÷ 1/6
Paso 1. Dale la vuelta a la segunda fracción (se convierte en una recíproca):
1/6 se convierte en 6/1
Paso 2. Multiplique la primera fracción por ese recíproco:
(multiplica las puntas …)
1/2 × 6/1 = (1 × 6) / (2 × 1) = 6/2
(… multiplique los fondos)
Paso 3. Simplifique la fracción:
6/2 = 3
Otro ejemplo:
1/8 ÷ 1/4
Paso 1. Dele la vuelta a la segunda fracción (la recíproca):
1/4 se convierte en 4/1
Paso 2. Multiplique la primera fracción por ese recíproco:
1/8 × 4/1 = (1 × 4) / (8 × 1) = 4/8
Paso 3. Simplifiqie la fracción:
4/8 = 1/2
Ejercicios de división de fracciones
Método 1: invertir y multiplicar
Para dividir fracciones, tome el recíproco (invierta la fracción) del divisor y multiplique el dividendo. Esta es la técnica más rápida para dividir fracciones. La parte superior e inferior se multiplican por el mismo número y, dado que ese número es el recíproco de la parte inferior, la parte inferior se convierte en uno. Dividir cualquier cosa por uno deja el valor «cualquier cosa» igual.
Método 2: denominador común
Existe una forma más extensa de dividir fracciones y podría decirse que es un método «más correcto». Implica el uso de fracciones equivalentes para hacer iguales los denominadores de ambas fracciones. Esta es la forma correcta ya que, estrictamente hablando, no se pueden dividir manzanas por naranjas de la misma manera que no se pueden dividir quintos por cuartos.