Actualizado 14 diciembre, 2020
En la geometría, el cuadrilátero es una de las figuras más conocidas y se trata de un polígono que posee cuatro ángulos y cuatro lados. Dentro de los cuadriláteros podemos encontrar a los paralelogramos, los trapecios y los trapezoides.

¿Qué es un cuadrilátero?
Se denomina cuadrilátero a aquellas figuras geométricas planas y cerradas en cuatro lados. La palabra cuadrilátero deriva del latín quadrilatĕrus.
Estas figuras geométricas pueden tener diferentes formas pero todas cumplen con ciertos requisitos, los cuales son: cuatro vértices, cuatro lados, dos diagonales y la característica de que la suma de sus ángulos internos siempre da como resultado 360°. Además se puede afirmar que los cuadriláteros son cuadrángulos, ya que los mismos son polígonos que poseen cuatro ángulos.
Según establece la geometría planteada por Euclides, los cuadriláteros son polígonos que poseen cuatro vértices y cuatro lados. Estas figuras geométricas son figuras planas y se encuentran delimitadas por cuatro segmentos de recta que son denominados lados y que se interceptan en cuatro puntos no alineados, denominados vértices. En resumen, todos los cuadriláteros tienen cuatro lados, cuatro ángulos interiores, cuatro ángulos exteriores, cuatro vértices y dos diagonales, que son los segmentos que unen los vértices opuestos.
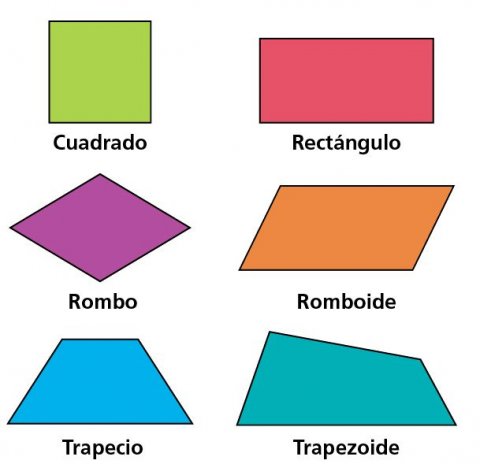
Elementos de los cuadriláteros
Dentro de los elementos o características principales de esta figura geométrica, podemos encontrar:
–Cuatro lados: todos se encuentran unidos por los vértices contiguos. Son las líneas o los segmentos que se unen a los vértices. Pueden o no ser iguales entre sí, esto dependerá del tipo de cuadrilátero.
–Cuatro vértices: o también llamados puntos de intersección de los lados que lo conforman.
–Dos diagonales: las mismas se forman por segmentos cuyos extremos son dos vértices no contiguos.
–Cuatro ángulos interiores: los mismos están formados por dos lados contiguos.
–Cuatro ángulos exteriores: estos ángulos son determinados por la prolongación de cada uno de los lados sobre un vértice.
Los ángulos además pueden ser, rectos, agudos u obtusos.
Propiedades y características de los cuadriláteros
Dentro de las principales características de los cuadriláteros podemos encontrar:
-La suma total de los ángulos internos de un cuadrilátero convexo es igual a 360º; es decir A + B + C + D = 360º.
-Las diagonales de un cuadrilátero siempre convexo se cortan.
-Todo cuadrilátero convexo puede definirse como la unión de dos triángulos con lado común en una de las diagonales.
-Si unimos con cuatro segmentos los puntos medios de todos los lados de un cuadrilátero, dichos segmentos formaran un paralelogramo.
-Si hay un segmento por la intersección de las diagonales de un cuadrilátero y el mismo une dos lados opuestos, determinará dos cuadriláteros con un lado común.
-Si un cuadrilátero está circunscrito, significa que la suma de sus lados opuestos es igual. Esto quiere decir que AB + CD = BC + DA.
-Si un cuadrilátero está inscrito en una circunferencia, la suma de sus ángulos opuestos será igual a 180º.
-Si ABCD es un cuadrilátero inscrito, AB es su diámetro, por lo tanto las proyecciones de sus lados AD y BC sobre la recta CD serán iguales.
Clasificación de los cuadriláteros
Los cuadriláteros cuando son simples se pueden dividir en dos tipos: los cuadriláteros cóncavos y los cuadriláteros convexos.
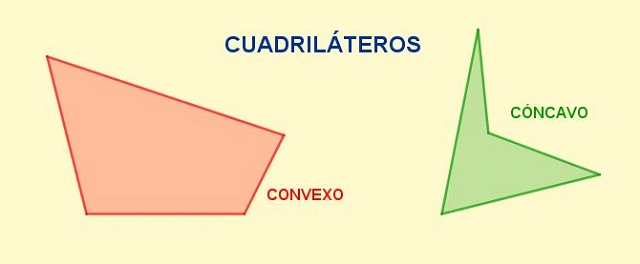
Los cuadriláteros cóncavos son aquellos en los que por lo menos uno de sus ángulos interiores mide más de 180°. Este tipo de cuadrilátero es reconocible ya que al trazar una línea recta los lados de la figura rozarán en más de dos puntos a este cuadrilátero.
Los cuadriláteros convexos son aquellos que no poseen ningún ángulo interior que supere los 180° de medida. Este tipo de cuadrilátero es reconocible fácilmente ya que si se traza una línea por el medio del cuadrilátero convexo siempre se cortará la figura en dos puntos.
Tipos de cuadriláteros
Los cuadriláteros se caracterizan por el paralelismo de sus lados. Por esta razón es que podemos mencionar que existen distintos tipos de cuadriláteros, los cuales son: paralelogramos (donde los lados opuestos son paralelos dos a dos), trapezoides (no tiene lados paralelos) y trapecios (tienen sólo dos lados opuestos paralelos). A continuación detallamos cada uno de ellos:
Paralelogramo
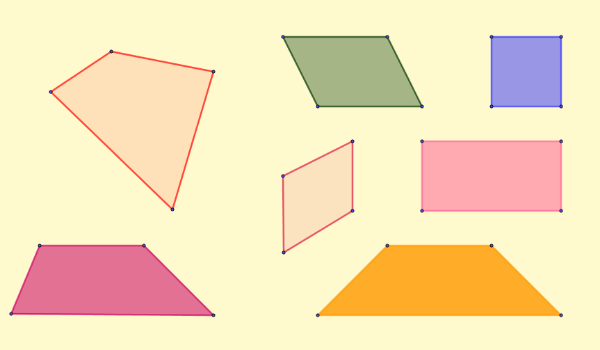
Se denomina paralelogramo al cuadrilátero que tiene dos pares de lados paralelos y además poseen la misma longitud. Las diagonales de los paralelogramos se cortan en el punto medio y sus ángulos opuestos son iguales. Ejemplos claros de paralelogramos son el cuadrado, el rectángulo, el rombo y el romboide. Veamos el concepto de ellos:
-Los rectángulos: aquellos que tienen los cuatro ángulos iguales. Podemos definir al rectángulo como un polígono, cuadrilátero y paralelogramo, en donde sus lados opuestos son iguales y paralelos y sus ángulos son rectos.
-Los rombos: los rombos se clasifican como un polígono, cuadrilátero y paralelogramo, en los cuales sus cuatro lados son iguales, sus lados opuestos entre sí, y sus ángulos no son necesariamente rectos. Sus ángulos opuestos y sus diagonales son perpendiculares entre sí.
-Los cuadrados: aquellos paralelogramos que tienen los cuatro ángulos iguales y los cuatro lados iguales. Este paralelogramo cumple con la característica de ser cuadrilátero, rectángulo y rombo al mismo tiempo, ya que sus cuatro ángulos son iguales y rectos.
-Los romboides: son los paralelogramos propiamente dichos, es decir, los que no son rectángulos, ni rombos, ni cuadrados. Sus lados opuestos son iguales entre sí, al igual que sus ángulos opuestos. Por otro lado sus diagonales no son perpendiculares tal como es el caso del rombo, ya que sus lados adyacentes son distintos.
Además, todos los paralelogramos poseen las siguientes propiedades:
-Los lados opuestos poseen la misma longitud.
-Los ángulos opuestos son iguales.
-Las diagonales se cortan en su punto medio.
Trapecio
Los trapecios son aquellos cuadriláteros que tienen dos lados paralelos opuestos, de distinta longitud. Los otros dos lados son paralelos.
Esta figura geométrica tiene la apariencia de un cuadrilátero no regular donde sólo dos lados son paralelos. Aquellos que son paralelos están considerados como bases y entre ellos se establece una distancia que se denomina altura. El segmento cuyos bordes son los puntos medios de los lados que no son paralelos se denomina como mediana.
Los trapecios además poseen la siguiente clasificación, según el análisis de sus ángulos interiores:
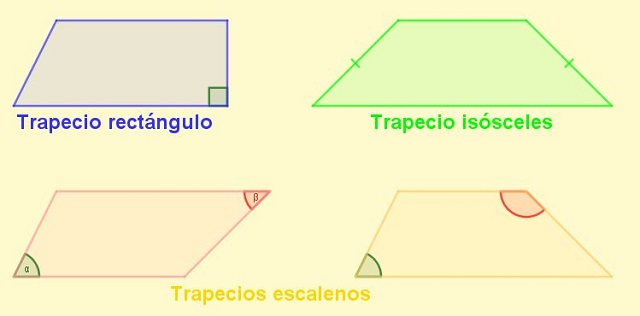
–Trapecio rectángulo: aquellos que tienen dos ángulos rectos en su interior, otro agudo y el restante obtuso.
–Trapecios isósceles: aquellos en donde sus lados paralelos no son de igual longitud. Se denomina isósceles a los trapecios que poseen un par de ángulos interiores agudos y los restantes obtusos.
–Trapecio escaleno: aquellos que no son trapecios rectángulos ni trapecios isósceles. En esta clasificación se incluye a los trapecios que tienen todos los ángulos de su interior de diferente amplitud.
Trapezoide
Los trapezoides son los rectángulos que carecen de lados paralelos. Un claro ejemplo de ellos son el trapezoide simétrico y el trapezoide asimétrico.
El trapezoide es un polígono, es decir una figura plana que se califica como un cuadrilátero irregular, esto quiere decir que poseee cuatro lados que no son iguales.
Los trapezoides de clasifican en:
–Simétricos: también denominados “cometa”. Estos trapezoides se identifican porque son simétricos respecto a lo que es la diagonal mayor, tiene dos pares de lados consecutivos iguales y además tiene un par de ángulos opuestos que también son iguales. Otra de sus características principales es que sus diagonales son perpendiculares.
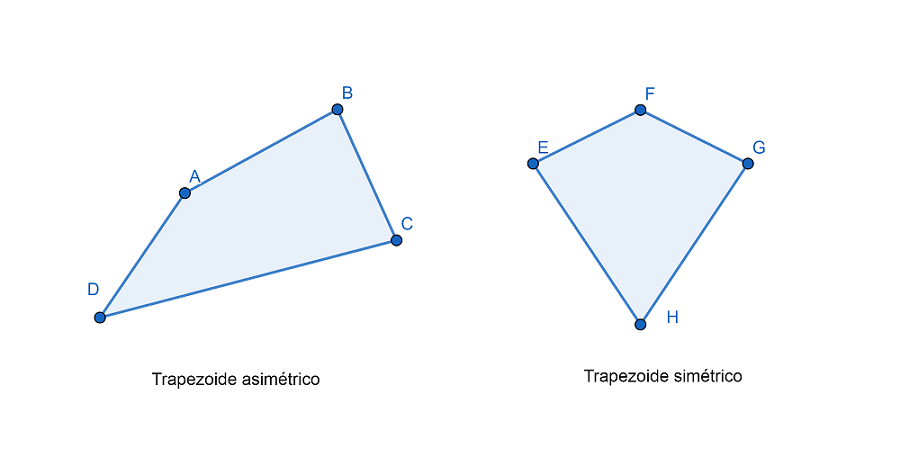
–Asimétricos o amorfo: aquellos que no poseen una forma definida. Esta figura también es conocida con el nombre de trapezoide escaleno y su característica principal es que todos sus lados son distintos.