Actualizado 29 junio, 2021
Una distribución de frecuencia muestra, valga la redundancia, la frecuencia de elementos repetidos en forma gráfica o tabular. Ofrece una visualización de la frecuencia de los elementos o muestra el número de veces que ocurrieron. Desde representar el desempeño de las clases en las escuelas hasta mostrar datos estadísticos en otros campos, existen varias aplicaciones para las tablas y gráficos de distribución de frecuencia. Cuando se trata de finanzas, los comerciantes las utilizan para tomar nota de los precios y otros detalles y también para identificar tendencias. Por lo tanto, es un concepto importante en matemáticas.
¿Qué es la distribución de frecuencias?
La distribución de frecuencia se utiliza para organizar los datos recopilados en forma de tabla. Los datos pueden ser calificaciones obtenidas por los estudiantes, temperaturas de diferentes pueblos, puntos obtenidos en un partido de voleibol, etc. Después de la recolección de datos, tenemos que mostrarlos de manera significativa para una mejor comprensión. Organice los datos de tal manera que todas sus características se resuman en una tabla.
Consideremos un ejemplo para entender esto mejor. Los siguientes son los puntajes de 10 estudiantes de matemática de la clase del Sr. Chris 15, 17, 20, 15, 20, 17, 17, 14, 14, 20. Representemos estos datos en forma de tabla y averigüemos la frecuencia de estudiantes que obtuvieron las mismas calificaciones.
| Calificaciones del examen | Número de alumnos |
| 15 | 2 |
| 17 | 3 |
| 20 | 3 |
| 14 | 2 |
Podemos ver que todos los datos recopilados están organizados bajo los títulos «calificaciones del examen» y «número de estudiantes». Esto facilita la comprensión de la información proporcionada y podemos ver el número de alumnos que obtuvieron las mismas notas.
Por lo tanto, la distribución de frecuencia en las estadísticas nos ayuda a organizar los datos de una manera fácil para comprender sus características de un vistazo.
¿Qué son las tablas de frecuencia o distribución de frecuencias?
Una tabla de distribución de frecuencia es un gráfico que muestra la frecuencia de un elemento que aparece varias veces en un conjunto de datos. Consideremos un ejemplo para entender esto mejor. Un frasco que contiene cuentas de diferentes colores: rojo, verde, azul, negro, rojo, verde, azul, amarillo, rojo, rojo, verde, verde, verde, amarillo, rojo, verde, amarillo.
Para saber el número exacto de cuentas de cada color en particular, necesitamos clasificar las cuentas en categorías. Una manera fácil de encontrar la cantidad de cuentas de cada color es usar marcas de conteo. Elija las cuentas una por una e ingrese las marcas de conteo en la fila y columna respectivas. Luego, indique la frecuencia de cada elemento de la tabla.
Tipos de frecuencias
Hay cuatro tipos de distribución de frecuencias en las estadísticas.
- Distribución de frecuencia no agrupada: la distribución de frecuencia no agrupada muestra la frecuencia de un elemento en cada valor de datos por separado en lugar de grupos de valores de datos.
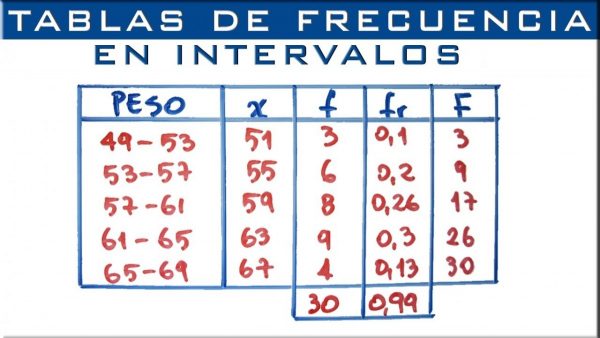
- Distribución de frecuencia agrupada: en una distribución de frecuencia agrupada, los datos se organizan y separan en grupos denominados intervalos de clase. La frecuencia de los datos que pertenecen a cada intervalo de clase se anota en una tabla de distribución de frecuencia. La tabla de frecuencias agrupadas muestra la distribución de frecuencias en intervalos de clase.
- Distribución de frecuencia relativa: una distribución de frecuencia relativa indica la proporción del número total de observaciones asociadas con cada categoría.
- Distribución de frecuencia acumulada: una distribución de frecuencia acumulada es la suma de la primera frecuencia y todas las frecuencias por debajo de ella en una distribución de frecuencia. Debe agregar un valor con el siguiente valor, luego agregar la suma con el siguiente valor nuevamente y así sucesivamente hasta el último. La última frecuencia acumulada será la suma total de todas las frecuencias.
Tipos de tabla de distribución de frecuencia
Hay dos tipos de tablas de distribución de frecuencia: tablas de distribución de frecuencia agrupadas y no agrupadas.
Tabla de distribución de frecuencia agrupada
Para organizar una gran cantidad de observaciones o datos, utilizamos una tabla de distribución de frecuencia agrupada. En esto, formamos intervalos de clase para contar la frecuencia de los datos que pertenecen a ese intervalo de clase en particular.
Por ejemplo, las notas obtenidas por 20 estudiantes en la prueba son las siguientes. 5, 10, 20, 15, 5, 20, 20, 15, 15, 15, 10, 10, 10, 20, 15, 5, 18, 18, 18, 18. Para organizar los datos en una tabla agrupada tenemos que hacer intervalos de clases. Por lo tanto, crearemos intervalos de clase como 0-5, 6-10, etc.
La siguiente tabla muestra dos columnas, una es de intervalos de clase (calificaciones obtenidas en la prueba) y la segunda es de frecuencia (número de estudiantes).
| Calificaciones obtenidas en la prueba | Número de estudiantes |
| 0 – 5 | 3 |
| 6 – 10 | 4 |
| 11 – 15 | 5 |
| 16 – 20 | 8 |
Tabla de distribución de frecuencia no agrupada
En la tabla de distribución de frecuencia desagrupada, no hacemos intervalos de clase, escribimos la frecuencia precisa de los datos individuales. Teniendo en cuenta el ejemplo anterior, la tabla desagrupada será así.
La siguiente tabla muestra dos columnas: una es de calificaciones obtenidas en la prueba y la segunda es de frecuencia (número de estudiantes).
| Calificaciones obtenidas en la prueba | Número de estudiantes |
| 5 | 3 |
| 10 | 4 |
| 15 | 5 |
| 18 | 4 |
| 20 | 4 |
Gráficos de distribución de frecuencia
Hay otra forma de mostrar datos en forma de gráficos y se puede hacer utilizando un gráfico de distribución de frecuencia. Los gráficos nos ayudan a comprender los datos recopilados de una manera sencilla. La representación gráfica de los datos se puede mostrar usando lo siguiente:
- Gráficos de barras: los gráficos de barras representan datos utilizando barras rectangulares de ancho uniforme. El espacio entre dichas barras es el mismo.
- Histogramas: un histograma es una presentación gráfica de datos que utiliza barras rectangulares de diferentes alturas. En un histograma, no hay espacio entre las barras rectangulares.
- Gráfico circular: Registra datos de manera circular y luego se divide en sectores que muestran una parte del conjunto de los datos.
- Polígono de frecuencia: un polígono de frecuencia se dibuja uniendo los puntos medios de las barras en un histograma.
¿Cómo crear una tabla de frecuencias para datos agrupados?
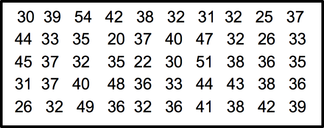
Suponga que queremos identificar la edad de 50 estudiantes en la clase de Estadística. Primero tendríamos que obtener los datos sobre las edades de los estudiantes. Cuando estos están en su forma original, se denominan datos brutos y se enumeran a continuación.
Después de recopilar datos, tendremos una gran masa de datos en forma cruda y desorganizada. Para organizar los datos, debemos seguir los siguientes pasos
Pasos para organizar datos:
- Organizar los datos en una matriz
- Decidir el número de clases (k)
- Calcular el intervalo de clases
- Prepare una hoja de recuento
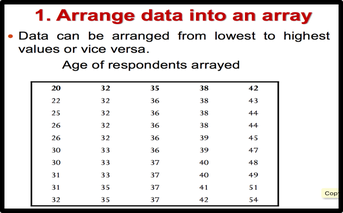
1. Organice los datos en una matriz: El primer paso para organizar los datos es organizarlos en una matriz para que podamos observar los datos de una manera más significativa y sistemática. Tenga en cuenta que los datos pueden ordenarse de menor a mayor valor (orden ascendente) o de mayor a menor valor (orden descendente).
2. Decidir el número de clases (k): Antes de construir las clases, debemos decidir el número de clases. Como guía general, el número de clase recomendado debe estar entre 5 y 20. Sin embargo, es solo una guía. El número de clase puede ser menor de 5 o más de 20. Otra pauta que se puede utilizar para decidir el número de clases es utilizar la regla de Sturges.
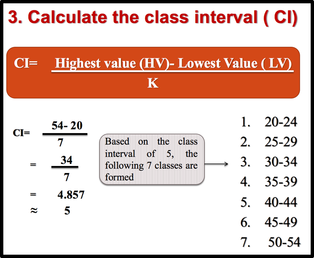
3. Calcule el intervalo de clase (CI)
4. Prepare una hoja de recuento: Una hoja de recuento es importante para calcular la frecuencia de casos en cada una de las siete clases.
En la distribución anterior, los valores 20 y 24 de la primera clase se denominan límites de clase. El límite de clase inferior es 20; representa el valor de datos más pequeño que se puede incluir en la clase. El límite de clase superior es 24; representa el valor de datos más grande que se puede incluir en la primera clase.
Límites de clase: estos números se utilizan para separar las clases de modo que no haya huecos en la distribución de frecuencias. Las brechas se deben a los límites; por ejemplo, hay una brecha entre 24 y 25.
Podemos encontrar los límites restando 0.5 de 20 (el límite de clase inferior) y agregando 0.5 a 24 (el límite de clase superior). Tenga en cuenta que las clases deben ser mutuamente excluyentes. Las clases mutuamente excluyentes tienen límites de clase que no se superponen, por lo que los datos no se pueden colocar en dos clases.
Para encontrar los límites de las clases:
- Reste el primer límite de clase superior del segundo límite de clase inferior.
- Dividir la diferencia por 2
- Reste este valor de todos los límites de la clase inferior y agregue el valor a todos los límites de la clase superior.
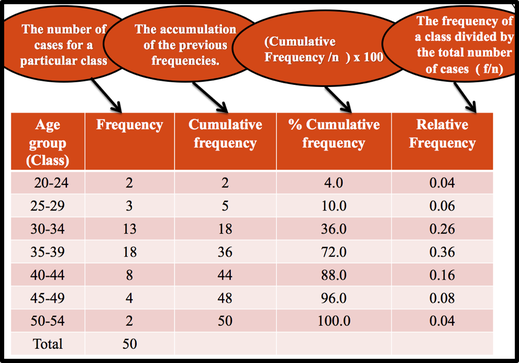
Una distribución de frecuencia acumulada (CF) es una distribución que muestra el número de valores de datos menores o iguales a un valor específico (generalmente un límite superior). Se obtiene sumando la frecuencia para esa clase y todas las clases anteriores. Naturalmente, una forma más corta de hacer esto sería simplemente agregar la frecuencia acumulada de la clase a continuación a la frecuencia de la clase dada. Por ejemplo, podemos decir que 18 (36%) estudiantes son menores o iguales a 34,5 años en la tercera clase. Alternativamente, 32 (64%) de los estudiantes tienen 34,5 años o más.
La frecuencia relativa muestra la proporción de valores de datos que pertenecen a una clase determinada. En alguna situación, la frecuencia relativa es más importante que el número real de valores de datos que caen en esa clase. Por ejemplo, si queremos comparar la distribución de edad de los estudiantes en la clase de estadística con la distribución de edad de los estudiantes en la clase de contabilidad, usaría distribuciones de frecuencia relativa. La razón es que dado que la población de estas dos clases es diferente. Para convertir una frecuencia en una proporción o frecuencia relativa, debemos dividir la frecuencia de cada clase por el total de las frecuencias. La suma de las frecuencias relativas siempre será 1.
¿Cómo crear una tabla de frecuencias para datos no agrupados?
1. Establezca los valores de los datos, que se denominan puntuaciones, en la columna comenzando desde el valor más bajo hasta el más alto o viceversa;
2. Cree la segunda columna con la frecuencia de cada ocurrencia de datos. Esta columna se conoce como el recuento de puntuaciones;
3. Cree la tercera columna, donde se insertará la frecuencia relativa de cada puntaje. La frecuencia relativa se puede obtener de la siguiente manera: fr = f / N, allí f es la frecuencia de cada puntaje (de la segunda columna) y N es el número total de puntajes. Para verificar la exactitud de los cálculos, la suma de fr debe calcularse y debe ser igual a 1.
4. Se creará la siguiente columna, donde la frecuencia relativa se realizará en porcentajes.
5. En la siguiente columna, conocida como columna de frecuencia acumulada, se debe estimar la frecuencia acumulada para cada puntaje. Esta debe comenzar desde el valor más bajo de puntuación, para el cual la frecuencia acumulada es igual al valor de frecuencia de la segunda columna. Los cálculos adicionales deben realizarse para cada puntaje en una secuencia de menor a mayor y la frecuencia acumulada para cada puntaje siguiente es igual a la suma de la frecuencia acumulada del puntaje anterior y la frecuencia de este puntaje (de la segunda columna). La frecuencia acumulada de la puntuación más alta debe ser igual al número total de puntuaciones.
6. La siguiente columna se llama «proporción acumulada» y los valores de su columna se obtienen como una razón de frecuencia acumulada para cada puntaje y el número total de puntajes.
7. La última columna es el porcentaje acumulado, donde la proporción acumulada se presenta como porcentajes.
Ejemplos de tablas de frecuencia
Ejemplo 1
Suponga que las edades del publico en un partido de fútbol 5 se dan de la siguiente manera:
25,65,03,12,35,46,67,56,00,31,17
Este tipo de datos está en forma sin procesar y se conoce como datos sin procesar. La diferencia entre la medida del valor más alto y más bajo en una colección de datos se conoce como rango. Aquí, el rango es- | 67–00 |, es decir, 67
Cuando aumenta el número de observaciones, este tipo de representación es bastante agitado y los cálculos basados en esto pueden resultar bastante complejos. Como las estadísticas tratan sobre la presentación de datos en forma organizada, la representación de datos en forma tabular es más conveniente.
Considerando otro ejemplo: En un cuestionario, las calificaciones obtenidas por 20 estudiantes son:
12,15,15,29,30,21,30,30,15,17,19,15,20,20,16,21,23,24,23,21
Estos datos se pueden representar en forma de tabla de la siguiente manera:
| Calificaciones obtenidas | Número de estudiantes |
| 12 | 1 |
| 15 | 4 |
| 16 | 1 |
| 17 | 1 |
| 19 | 1 |
| 20 | 2 |
| 21 | 3 |
| 23 | 2 |
| 24 | 1 |
| 29 | 1 |
| 30 | 3 |
El número de veces que ocurre un dato en un conjunto de datos se conoce como frecuencia de datos. En el ejemplo anterior, la frecuencia es el número de estudiantes que obtuvieron varias calificaciones tabuladas. Este tipo de recopilación de datos tabulares se conoce como tabla de frecuencia no agrupada.
¿Qué pasa si en lugar de 20 estudiantes, 200 estudiantes toman la misma prueba? ¿Habría sido fácil representar esos datos en el formato de una tabla de distribución de frecuencias no agrupada? Bueno, obviamente no. Para representar una gran cantidad de información, los datos se subdividen en grupos de tamaños similares conocidos como clase o intervalos de clase y el tamaño de cada clase se conoce como ancho de clase o tamaño de clase.
Ejemplo 2
Para una mejor comprensión, considere la siguiente tabla que representa la altura de 200 estudiantes de secundaria.
Tabla de distribución de frecuencia agrupada
| Altura de los estudiantes (en cm) | Número de estudiantes |
| 130 – 139 | 19 |
| 140 – 149 | 42 |
| 150 – 159 | 35 |
| 160 – 169 | 78 |
| 170 – 189 | 26 |
La primera columna de la tabla representa el intervalo de clase con un ancho de clase de 10. En cada clase, el número más bajo indica el límite de clase inferior y el número más alto indica el límite de clase superior. Para la clase 150-159, el límite de clase inferior es 150 y el límite de clase superior es 159. Esto se conoce como distribución de frecuencia agrupada.
Ejemplo 3
Estos son los números de periódicos vendidos en una tienda local durante los últimos 10 días: 22, 20, 18, 23, 20, 25, 22, 20, 18, 20
Contemos cuántos de cada número hay:
| Periódicos vendidos | Frecuencia |
| 18 | 2 |
| 19 | 0 |
| 20 | 4 |
| 21 | 0 |
| 22 | 2 |
| 23 | 1 |
| 24 | 0 |
| 25 | 1 |
También es posible agrupar los valores. Aquí están agrupados en 5:
| Periódicos vendidos | Frecuencia |
| 15 – 19 | 2 |
| 20 – 24 | 7 |
| 25 – 29 | 1 |