Actualizado 19 abril, 2021
Las fracciones representan una cantidad numérica que forma parte de un objeto completo. Son elementos de las matemáticas que representan una proporción determinada entre dos cifras. Dentro del mundo de las fracciones podemos encontrar dos grandes clasificaciones: las fracciones homogéneas y las fracciones heterogéneas. A continuación conoceremos en detalle cada una de ellas.
¿Qué son las fracciones?
Las fracciones son el cociente entre dos números enteros y representan partes de una unidad.
Toda fracción esta compuesta por dos términos:
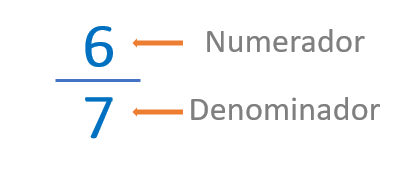
-El termino que indica el número de partes en las que se divide la unidad que se llama DENOMINADOR.
-El término que representa el número de partes a las que nos referimos se llama NUMERADOR.
Las fracciones pueden expresarse de las siguientes maneras:
-Como partes de una unidad: por ejemplo podemos indicar que nos comemos la mitad de una pizza o bien que leemos un cuarto de un libro.
-Como un cociente entre dos números: por ejemplo si tenemos dinero para repartir entre tantas personas, la fracción obtenida representará la cantidad de dinero que podemos darle a cada persona.
-Como fracción de cantidades: por ejemplo si sabemos que en una clase asisten 30 personas y queremos representar a dos tercios de los asistentes, entonces tendremos 2/3 * 30, sabremos que hay 20 personas en la clase.
Luego de este breve repaso podremos enfocarnos detalladamente en los conceptos de fracciones homogéneas y heterogéneas.
Fracciones homogéneas y heterogéneas
Estos conceptos definen un tipo de relación que existe entre dos o más fracciones y el mismo dependerá del denominador que tengan dichas fracciones. Por lo tanto:
–Dos fracciones son homogéneas cuando sus denominadores son iguales. Esto quiere decir que la unidad de ambas esta dividida en la misma cantidad de parte y es por eso que sus denominadores son iguales. Por ejemplo:
Si vemos las fracciones 2/5 y 4/5, podemos observar que son dos fracciones diferentes pero con igual denominador, por lo tanto son fracciones homogéneas.
–Dos fracciones son heterogéneas cuando sus denominadores son diferentes. Esto quiere decir que la unidad esta dividida que una cantidad diferentes de partes y por ende sus denominadores son diferentes. Por ejemplo:
Si vemos las fracciones 4/6 y 5/7 podemos observar que son dos fracciones diferentes y con denominadores diferentes, por lo tanto son fracciones heterogéneas.
Fracciones homogéneas
Dos fracciones o más son homogéneas cuando su denominador es el mismo, esto quiere decir que la unidad esta dividida en las mismas partes, por eso comparten el denominador. De lo contrario serán heterogéneas.
Sumas de fracciones homogéneas
Para realizar la suma de fracciones homogéneas, debemos sumar los denominadores y dejar el mismo denominador. Por ejemplo:
1/6 + 2/6 = nos dará un resultado de 3/6.
Resta de fracciones homogéneas
Para realizar la resta de fracciones homogéneas, se procede de la misma manera que para las sumas: se restan los numeradores y se deja tal cual el denominador. Por ejemplo:
6/5 – 3/5: tendremos como resultado la fracción de 3/5.
Multiplicación de fracciones homogéneas
Para realizar la multiplicación de fracciones que son homogéneas, es decir que tienen igual denominador, debemos hacer lo mismo que en el producto de fracciones son diferentes denominador. Por ejemplo:
Queremos multiplicar las fracciones 5/4 x 3/4. Entonces el numerador del resultado será el producto entre los denominadores (5 x 3 = 15). El denominador será los denominadores multiplicados (4 x 4 =16), que en este caso de fracciones homogéneas son iguales.
Luego verificamos si se puede simplificar o no la fracción y ya tendremos el resultado, que en nuestro ejemplo será: 15/16.
División de fracciones homogéneas
Para realizar la división de fracciones homogéneas, de igual modo que en las fracciones con igual denominador, tienen la siguiente formula:
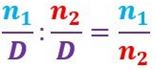
Se debe multiplicar en cruz, es decir multiplica arriba y abajo por D y luego se quita:
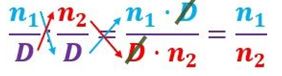
Veamos un ejemplo:
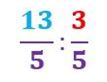
Obtendremos como resultado de la división, una fracción de términos 13 (el primer numerado) y de 3 el segundo.
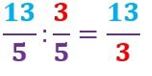
Fracciones heterogéneas
Dos fracciones o más son heterogéneas cuando tienen diferentes denominadores. Para poder realizar operaciones entre estas fracciones, como suma o resta, siempre se deberá buscar un común denominador, y el mismo se obtienen calculando el mínimo común múltiplo de los denominadores de aquellas fracciones que se quieren sumar o restar.
Suma de Fracciones Heterogéneas
Para sumar fracciones heterogéneas (es decir de aquellas fracciones que tienen diferente denominador), debemos comenzar por buscar la equivalencia entre las fracciones, con el objetivo de convertir la operación en una suma de fracciones de igual denominador. Para esto podemos optar por dos métodos: el método del mínimo común múltiplo de los denominadores o bien el método de la multiplicación en cruz.
Método de mínimo común múltiplo de los denominadores
Para encontrar un denominador común, debemos encontrar primero el mínimo común múltiplo de los denominadores de las fracciones que vamos a sumar. Por ejemplo tenemos la siguiente suma:
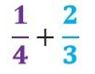
Como vemos, las fracciones tienen distinto denominador, por lo que necesitamos que todas tengan el mismo. Para eso primero debemos factorizar los dos denominadores:
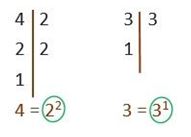
Una vez que tenemos la factorización, sacamos el mínimo común múltiplo (mcm) de ambos denominadores (4 y 3). El mcm, una vez realizada la factorización, son los factores comunes y no comunes elevados al máximo exponente. En nuestro ejemplo será:
Entonces podemos observar que el mínimo común múltiplo de los denominadores será 12. Por lo tanto los denominadores de las nuevas fracciones serán 12 y los numeradores serán el numerador inicial por 12 dividido entre el denominador inicial, es decir:
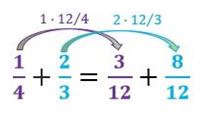De este modo tendremos las dos fracciones con el mismo denominador y podremos realizar la suma de ambas, dejando el denominador común y sumando los numeradores.
Método de la multiplicación en cruz
El otro método es el de la multiplicación en cruz y para esto debemos:
Siguiendo el siguiente ejemplo: Queremos sumar las fracciones siguientes que tienen distintos denominadores.
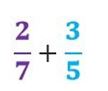
Lo primero a realizar será calcular el numerador multiplicando las fracciones en cruz, es decir el numerador de la primera por el denominador de la segunda y viceversa. Luego sumamos las dos multiplicaciones:
Luego buscamos el denominador de la fracción resultado que será el producto de los dos denominadores: 7 · 5 = 35. Por ende el resultado de esta suma será el siguiente:
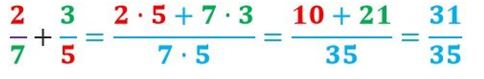
Resta de Fracciones Heterogéneas
Para restar fracciones heterogéneas debemos buscar también la equivalencia entre las fracciones y buscar el mínimo común múltiplo de los denominadores o bien el método de multiplicación en cruz. Una vez obtenido procedemos a la resta de las fracciones.
Multiplicación de fracciones heterogéneas
En el caso de la multiplicación de las fracciones heterogéneas, es de la misma manera que las homogéneas. El resultado de dos fracciones será otra fracción. El numerador serpa el producto de los numeradores y el denominador el producto de los denominadores.
Veamos un ejemplo para que quede bien claro. Tenemos la siguiente multiplicación de fracciones:
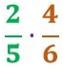
El numerador de la fracción que tendremos como resultado será el producto de sus numeradores (multiplicación de los números de arriba).
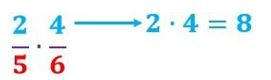
Por otro lado el denominador del resultado será el producto de los denominadores, es decir la multiplicación de los números de debajo de las fracciones que se multiplican.
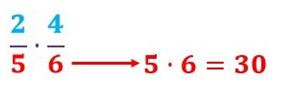
Una vez que tenemos los resultados de ambas multiplicaciones, lo que quedará será, en caso que se pueda, simplificar la fracción:
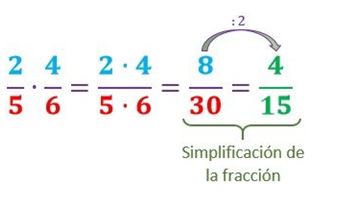
De este modo podemos obtener el resultado de la multiplicación de las fracciones heterogéneas.
División de fracciones heterogéneas
En el caso de la división de fracciones heterogéneas, procedemos al igual que en el productor a realizar la multiplicación en cruz. Esto quiere decir que el numerador (número de arriba) de la primera fracción se multiplica por el denominador (número de abajo) de la segunda fracción y así obtendremos el numerador. Luego para obtener el denominador, tenemos que multiplicar el denominador (número de abajo) de la primera fracción por el numerador (número de arriba) de la segunda fracción.