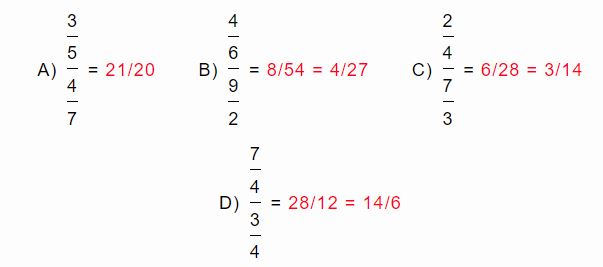Actualizado 25 febrero, 2023
La división es otra de las operaciones matemáticas que podemos realizar con las fracciones. El resultado de la misma será otra fracción que posee como numerador el producto del numerador del dividendo por el denominador del divisor y posee como denominador a la multiplicación del dividendo por el numerador del divisor.
En el día de hoy conoceremos como realizar las divisiones de fracciones por medio de los distintos métodos para realizar la operación.

¿Qué son las fracciones?
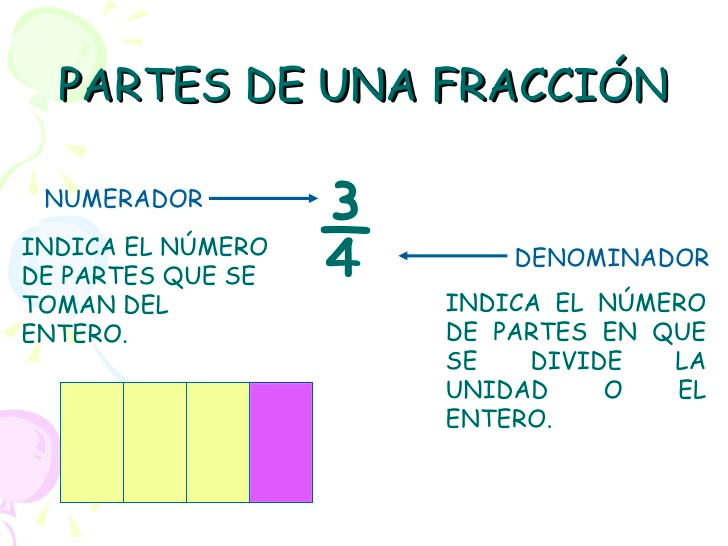
La fracción es una expresión que marca una división, por lo cual se puede afirmar que una fracción representa una porción de una unidad. Las mismas son expresadas con dos números separados por una barra horizontal.
El número que se encuentra por encima de dicha barra recibe el nombre de numerador y el numero que se encuentra por debajo de la barra divisora recibe el nombre de denominador.
¿Cómo se leen las fracciones? La forma de leer las fracciones es de la siguiente manera:
El numero que se encuentra en el numerador, es decir por encima de la barra horizontal, se lee tal cual conocemos al numero. El numero que se encuentra en el denominador, es decir por debajo de la barra divisora cambia de nombre y se deberán tener en cuenta los nombramientos que veremos a continuación:
- Nombramiento si el denominador va de dos a diez:
Si es 2 es «medios».
Si es 3 es «tercios».
Si es 4 es “cuartos”.
Si es 5 es “quintos”.
Si es 6 es “sextos”.
Si es 7 es “séptimo”.
Si es 8 es “octavos”.
Si es 9 es “novenos”.
Si es 10 es “décimos”.

- Nombramiento si el denominador es mayor a diez:
En este caso se considera el nombre habitual que conocemos del número pero a diferencia de los casos anteriores, se le agrega a dicho nombre la terminación “avos”, veamos algunos ejemplos
4/12 se puede leer como “cuatro doceavos”.
8/22 se puede leer como “ocho veintedosavos”.
3/60 se puede leer como “tres sesentavos”.
- Nombramiento si el denominador termina en 1 pero seguido solo de ceros:
Si es 10 es “décimos”.
Si es 100 es “centésimo”.
Si es 1 000 es “milésimo”.
Si es 10 000 es “diezmilésimo”.
Si es 100 000 es “cienmilésimo”.
Si es 1 000 000 es “»millonésimo”.
Cómo dividir dos fracciones?
Para dividir dos fracciones, se sigue la regla:
- Se invierte (se da vuelta) la segunda fracción, es decir, se intercambian el numerador y el denominador.
- Se multiplica la primera fracción por la fracción resultante de invertir la segunda fracción.
- Se simplifica la fracción resultante si es necesario.
Por ejemplo, para dividir las fracciones 2/3 y 4/5, se sigue los siguientes pasos:
- Se invierte la segunda fracción: 4/5 se convierte en 5/4.
- Se multiplica la primera fracción por la fracción resultante de invertir la segunda fracción:
2/3 ÷ 4/5 = 2/3 x 5/4
- Se simplifica la fracción resultante si es necesario:
2/3 x 5/4 = 10/12 = 5/6
Por lo tanto, la respuesta es 5/6.
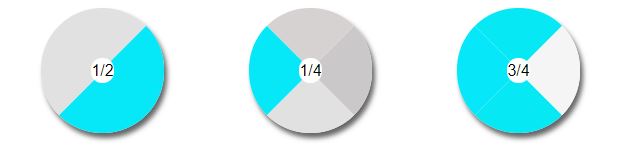
Representación gráfica de las fracciones
En cuanto a la forma para representar las diferentes fracciones, debemos saber que una fracción se puede representar de diversas formas dependiendo de las cantidades en las que se divida.
Divisiones de fracciones
A diferencia de las otras operaciones matemáticas que hemos visto con las fracciones, en la división no se realiza una repartición sino una multiplicación o también llamado producto, la cual implica multiplicar de manera cruzada los numeradores y los denominadores de ambas fracciones.
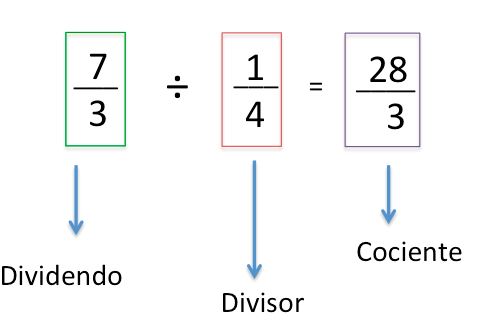
Para poder comenzar a realizar esta operación primero debemos conocer los términos de la división.
–Divisor: Es la cifra o la cantidad por la cual dividiremos, teniendo en cuenta las cantidades que nos indica el dividendo.
–Dividendo: Es la cantidad que queremos repartir y por la cual vamos a realizar la operación de división.
–Cociente: se llama así al resultado de la división.
¿Cómo dividir fracciones?
Para poder resolver divisiones de fracciones existen dos métodos diferentes. Veamos a continuación cada uno de ellos:
- Método de la división de fracciones con multiplicación en cruz
Este método consiste en multiplicar el numerador de la primera fracción por el denominador de la segunda fracción y el resultado de la multiplicación se ubicara en el numerado del resultado, por otro lado para poder obtener el resultado que se ubica en el denominador, debemos multiplicar el denominador de la primer fracción por el numerador de la segunda fracción. De este modo se esta aplicando lo que denomina multiplicación en cruz, se llama de dicha manera ya que tiene el siguiente esquema:
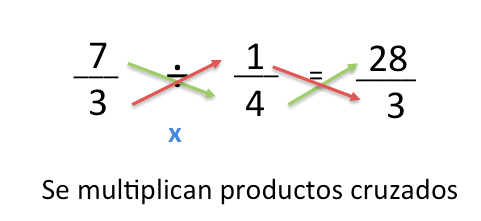
Vemos un ejemplo para entenderlo bien:
Tenemos para realizar la división entre las fracciones 1/3 (un tercio) y 2/6 (dos sextos), para poder realizar la operación debemos:
1.Debemos multiplicar el numerador de la primera fracción por el denominador de la segunda fracción.
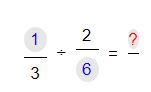
2.El resultado de dicha multiplicación entre el numerador de la primera fracción y el denominador de la segunda, se debe colocar en la posición del numerador del resultado.
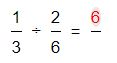
3.Una vez obtenido este primer resultado, continuaremos con la segunda multiplicación en cruz que es del denominador de la primera fracción por el numerador de la segunda fracción. El resultado del mismo se coloca en la ubicación del denominador del resultado.
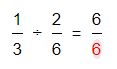
El resultado de esta división como vemos en 6/6, fracción que podemos simplificar porque tanto el numerador como el denominador tienen el mismo valor. El resultado final luego de la simplificación sería 6/6 = 1.
- Método de la división de fracciones por medio de la multiplicación de números internos y números externos.
Este método consiste en acomodar una fracción sobre otra para luego poder multiplicar los números externos del acomodo y obtener el resultado del numerador. Por otro lado multiplicamos los números internos del acomodo para poder obtener el resultado del denominador.
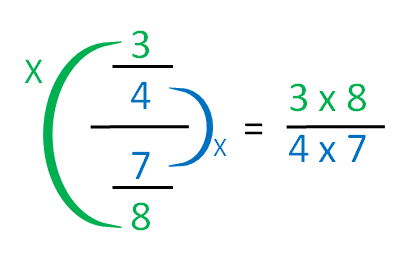
A continuación veremos como resolver por medio de este método la división de las fracciones 2/3 (dos tercios) y 1/4 (un cuarto).
1.Lo primero que debemos realizar será acomodar las fracciones una por encima de la otra para luego poder continuar con las multiplicaciones. Procederemos a ubicar la primer fracción de 2/3 sobre la segunda fracción de 1/4.
Un vez que tenemos las fracciones acomodadas, lo próximo que realizaremos será multiplicar los números externos.
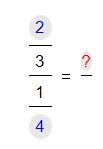
El resultado de este producto se ubicara en el numerador del resultado:
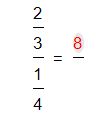
2.Una vez que tenemos este resultado, continuaremos con la multiplicación de los números internos y el resultado de dicho producto será ubicado en el denominador del resultado.
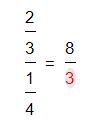
A continuación veremos un par de ejemplos para comprender bien el método numero dos
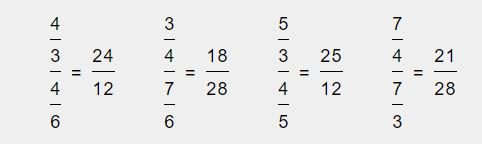
División de fracciones mixtas
Antes de explicar como realizar las divisiones de fracciones mixtas, repasaremos cuales son.
Las fracciones mixtas representan un número entero y una fracción propia, es decir comprende la suma de una parte entera más una fraccionaria. La fracción propia es aquella en donde el numerador de la misma es menor que su denominador.
Para poder realizar divisiones de fracciones mixtas es fundamental que la parte entera se exprese como una fracción con el mismo denominador que tiene la parte fraccionaria que la acompaña. Veámoslo con un ejemplo para poder comprenderlo bien.
Tenemos para realizar la división de las siguientes fracciones mixtas:
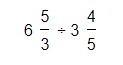
Lo primero que debemos realizar será convertir la parte entera que acompaña a ambas fracciones en una parte fraccionaria. Para esto tenemos que multiplicar la parte entera de cada una por el denominador de la fracción que lo acompaña.
De este modo nos quedarían las siguientes multiplicaciones:
6 x 3 = 18
3 x 5 = 15
Con estos nuevos resultados lo que debemos hacer es sumarlos a los números que figuran en los numeradores de cada una de las fracciones:
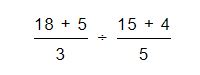
Como resultado de estas sumas tendremos las fracciones de 23/3 y 19/5.
Ahora si una vez convertidas podemos continuar con la división según el método que elijamos. En este caso lo haremos por el primer método que detallamos que es el de la cruz.
Por lo tanto vamos a multiplicar el numerador de la primera fracción por el denominador de la segunda y por otro lado multiplicamos el denominador de la primera fracción por el numerador de la segunda. Lo obtenido será el resultado de nuestra división original.
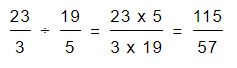
Ejercicios sobre división de fracciones
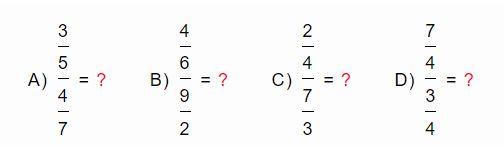
Resultados de los ejercicios